Research Areas
Sparsity and High-Dimensional Inference
My research addresses problems of large-scale data analysis through two approaches that have attracted considerable attention in recent years: sparsity-based Bayesian estimation methods and high-dimensional graphical models. My contributions include sharp asymptotic characterizations of many sparsity-based estimation algorithms. In addition, I have also developed a new approximate message passing methodology based on Gaussian approximations of loopy belief propagation that enables both computational efficiency and rich modeling flexibility that can extend spare estimation techniques to a great range of problems going forward.
Quantitative Inference in Neuroscience
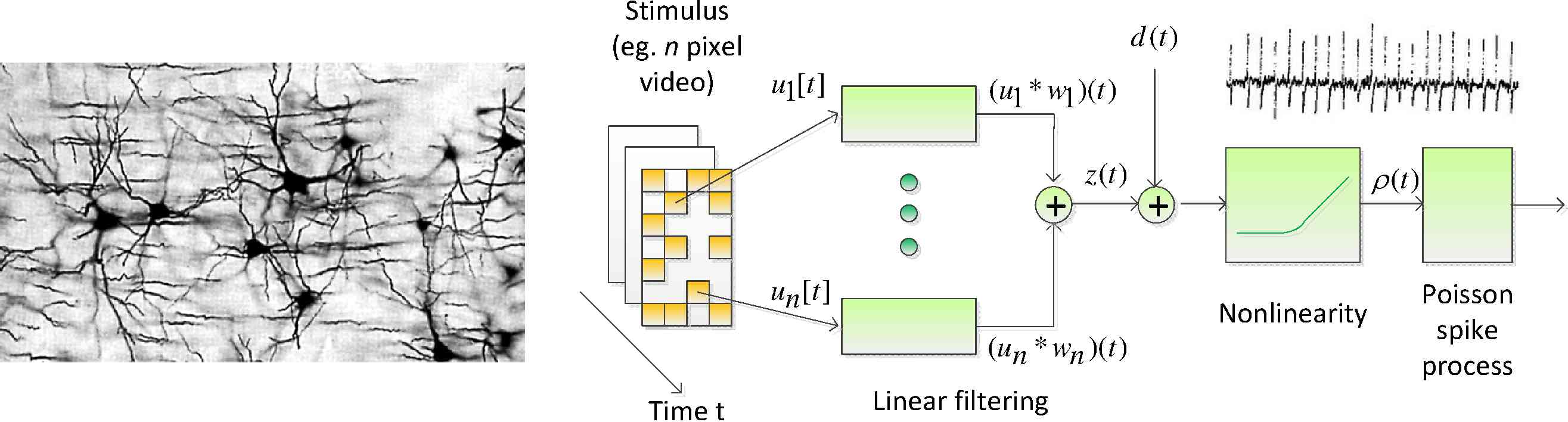
A key goal of computational neuroscience is to provide mathematical characterizations of underlying neuronal phenomena that give rise to behavioral complexities and cognition. Central to this project is the development of predictive network models. Toward this end, I have successfully applied sparsity-based estimation methods and graphical model techniques to problems in neural mapping and receptive field estimation. The techniques also show promise for dynamical systems modeling of epilepsy from high-resolution electrode arrays.
Optimization and Estimation in Dynamical Systems
This line of work considers estimation and learning of stochastic dynamical systems, particularly in linear state-space systems with with discrete random dynamics arising from switching and discrete events. For such systems, I developed a general linear matrix inequality-based analysis techniques and utilized this modeling and estimation framework toward improved design in audio compression, sensor networks, and robust communication.