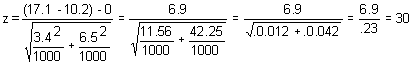
Sample Final Questions
1. There's lots going on here that can be distracting….Santa's personality, elves rebelling….but let's pick out of the stew what is relevant. Rudolf has a hypothesis: The elves tend to make certain toys when Santa is supervising and they tend to make different toys when Mrs. Claus is supervising.
What has Rudolf observed on three random days?
|
Type of toy made |
Santa Supervising |
Mrs. Claus supervising |
|
Stuffed animals |
16 |
7 |
|
Educational toys |
4 |
18 |
|
Other types of toys |
3 |
2 |
We're going to have to conduct a statistical test. In class we have learned the following:
|
Statistical procedure |
# of groups |
Size of sample |
Scaling of observations |
Statistical hypotheses* |
Type of hypothesis |
|
Confidence interval |
1 |
Confidence interval will be tighter as sample size increases |
Sum, count, %, average |
None |
What is our best bet of the location of the population parameter? |
|
One-sample z test |
1 |
Large, > 100 observations |
Sum, average (mean) |
H0: : obs = : exo H1: : obs ¹ : exo |
Is the difference between what we observe and what we think the parameter is consistent with chance? |
|
Two-sample z test |
2 |
Large, > 100 in each group |
Sum, Average (mean) |
H0: : 1 = : 2 H1: : 1 ¹ : 2 |
Is the difference observed between group 1 and group 2 consistent with chance differences between two independent draws out of a box? |
|
One-sample t-test |
1 |
Small, < 100 observations |
Average (mean) |
H0: : obs = : exo H1: : obs ¹ : exo |
Is the difference between what we observe and what we think the parameter is consistent with chance? |
|
Chi-square test |
1 or 2 |
Modest, ³ 5 per cell (not a hard and fast rule in this course) |
Counts, frequencies |
H0: fo - fe = 0, for all cells H1: fo - fe = 0, for at least one cell |
Is the difference between the observed distribution of frequencies in the cells consistent with the expected distribution predicted by the margins, except for chance? |
*Hypotheses depend upon the particular research question. I have shown only the most basic null hypothesis situation
The observations of toys are simple counts of the types of toys. There are two work groups (those working under Santa and those under Mrs. Claus). There are about 5 toys per cell on average. So it looks like a chi-square test would be appropriate.
So, first I state my research hypothesis:
The elves make different patterns of toys depending upon who is supervising them
Next my translation into statistical hypotheses
H0: fo - fe = 0, for all cells
H1: fo - fe = 0, for at least one cell
I plan to evaluate my null hypothesis at the P = .05 level. That means that when I calculate my chi-square value I will ask: Is the departure that I observe in cells counts different from what I expect to observe IF there is no difference in the elves behavior under the two different supervisors (that is IF the null hypothesis is absolutely, precisely true--no doubt about it) likely to occur simply by chance 5% or less of the time I make these observations.
Notice that the chance (5%) is not a statement about the chance that the null hypothesis is correct--I'm assuming it's absolutely correct under the null hypothesis. Notice also that the chance (5%) is not a statement about the probability that the alternative hypothesis is correct--I'll make my decision about the alternative hypothesis based on whether or not I reject the null hypothesis--I will only use logic and I will never know precisely how likely or unlikely I am to be correct in that decision.
You can think of it this way. Suppose for some reason I want to speak to your Dad. So I decide to go to your parents house and knock on the door. Suppose also that only one of two adults will come to the door and that the two adults are your parents and no one else. Then suppose that the physics department here has created an instrument that is a MOM detector. It gives a reading when held close to an adult of whether or not the person is a MOM. In the lab this instrument works really well. Moms average around 50 on the 100 scale and about 68% of moms score within a few points either way, though in testing it out in the field there is a great deal of variability in its readings simply due to chance samplings of the adult in question (better readings when she speaks and voice quality can be checked, worse readings if the adult is not thinking about her child perhaps studying at UCLA long into the night, etc.). No matter what the MOM meter reads there is always some possibility that it is reading a mom, though extreme readings either way are less likely to be a mom than readings right around the range in the center of the scale. Finally, suppose I send a little robot to your parents' door so I have no other input on which to make my decision except for readings from the MOM meter. I create the following hypotheses:
Null hypothesis: The adult who comes to the door is your MOM
Alternative hypothesis (and what I really want to make a decision about): The adult who comes to the door is your DAD
If the MOM meter tells me that the adult being observed has a 5% or less chance of being a mom
I reject the null. Notice, the person who comes to the door either is your mom or not--there is no chance involved. Five percent of the time when I make this decision, I am wrong, flat out wrong. If I reject the null, then logically only the alternative is left--it's your dad. Notice, I made the decision that it's your dad not on any DAD readings (I don't have a DAD meter). I decided that because it was very unlikely that adult I encountered was your mother it had to be your father.
If I don't reject the null--let's say there is a 25% chance it's your mom according to the MOM meter, I'm not saying for certain it is your mom, I'm just saying that it could be, might not be, I'm still uncertain--and because I haven't ruled out it being your mother I can't be sure it's your dad or not. Failing the reject the null is saying, well the extent of difference I'm observing in this reading on the MOM meter is not enough for me to conclude that it's not just a difference due to chance alone.
Our observations are like readings on a MOM meter. We never actually see the adult who comes to the door (that's the equivalent of being able to see the contents of the box). Instead we measure imprecisely from afar, and, given the uncertainty of our readings, come to a decision about the percent of time we would make these observations. If our readings suggest that it would be very rare, then we reject the chance only (null) hypothesis. If not rare, under chance, the we fail to reject it.
Now I calculate a few things to help me set up the table to calculate my chi-square
|
Type of toy made |
Santa Supervising |
Mrs. Claus supervising |
Total types of toys made |
|
Stuffed animals |
16 |
7 |
23 |
|
Educational toys |
4 |
18 |
22 |
|
Other types of toys |
3 |
2 |
5 |
|
Total toys made |
23 |
27 |
50 toys total |
The expected cell count (fe) for each cell is its row total times its column total divided by the total number of toys made
|
Cell |
fo |
fe |
fo - fe |
(fo - fe)2 |
(fo - fe)2/ fe |
|
Stuffed animal-Mr Claus |
16 |
(23*23)/50=10.58 |
5.42 |
29.38 |
2.78 |
|
Stuffed animal-Mrs. C |
7 |
(23*27)/50=12.42 |
-5.42 |
29.38 |
2.36 |
|
Ed toys-Mr. Claus |
4 |
(22*23)/50=10.12 |
-6.12 |
37.45 |
3.70 |
|
Ed toys-Mrs. Claus |
18 |
(22*27)/50=11.88 |
6.12 |
37.45 |
3.15 |
|
Others-Mr. Claus |
3 |
(5*23)/50=2.30 |
0.7 |
0.49 |
0.21 |
|
Others-Mrs. Claus |
2 |
(5*27)/50=2.70 |
-0.7 |
0.49 |
0.18 |
|
Chi-square is the sum of the last column: |
12.38 |
||||
Now I have to figure out my degrees of freedom:
The degrees of freedom are (number of rows - 1)(number of columns - 1) or (3 - 1)(2 - 1) = 2
Now I look up the chi-square value in the table:
Under 2 degrees of freedom the critical chi-square value is 5.99. So I need my chi-square value that I calculated must be that bigger or bigger for me to reject the null hypothesis.
Decision concerning my statistical hypotheses:
The chi-square is 12.38 with 2df. It exceeds the critical chi-square of 5.99. So I reject my null hypothesis. It still could be right; there is a small percentage of chance that it is. Instead I accept the alternative hypothesis: there is a real difference, not just due to chance, between what observe and what I expect to observe.
Conclusion:
In plain English, the elves are adjusting what toys they make depending up who is supervising them. When Santa's in charge they make the stuffed animals he likes; when Mrs. Claus is in charge the elves make more of the educational toys that she prefers.
2. What do we know? Inflation is 2 SD up. There is a relationship (r = -.6) between inflation and optimism. So when inflation is high people are more pessimistic. So we expect them to score lower on an optimism scale. Remember the relationship: predicted SD of one variable = correlation of the two variables * SD of the other variable. So we predict optimism should be, on average, about -6 * 2 or 1.2 SD below average.
We draw a sample of 1000 people. That's large and suggests that the relationships we're predicting should hold fairly well. Does the number 1000 mean anything for calculations we have to do--no, not this time. If the average mean is 100 and we expect the sample to be 1.2 SD below average, then we could predict the mean to be 100 + (-1.2)(15) or 82.
3. Well let's look at each option:
a. False--We never test the alternative hypothesis
b. True--the very small P value means if the null hypothesis is true then the chances that we would observe a difference this large is very, very rare. Which means that it is likely that something other than chance alone has contributed to the difference.
c. False--the outcome is rare under chance, not common. You have mixed up z and P.
d. False--we can't ever prove the null hypothesis. Think about it. We sample two groups twice out of the same box and their means are the same, fine; but we can also sample two groups out of two different boxes and their means are the same--it doesn't mean they come from the same box. All we could say is that it's possible, with the same means they come from the same box.
e. False--Power is the ability to detect a difference as not due to chance when in the fact the difference is not due to chance. Our small P indicates that we have sufficient power.
4. Here we have two groups and we want to test for differences between them. The two groups are measured in such a way that we know their means and standard deviations. The groups are large. So looking in the chart above, it appears that we should conduct a two-sample z-test.
Research hypothesis:
College students study longer hours than high school students
Translated into statistical hypotheses:
It's one-tailed (because we said one group is more than the other--we predict a direction)
H0: : 1 # : 2, there is no difference between the two means except due to chance
H1: : 1 > : 2, the mean for college students is in fact greater than the mean for high school students
Statistical test:
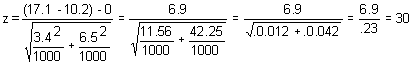
A z value this large or larger has a P value that is extremely small, close to but not zero.
Conclusion:
Reject the null. There appears to be a difference between the two groups that is not just chance. Looking at the means, I can interpret that difference as : College students do study longer hours than high school students.
5. We have a small sample of 8 observations. It is one group. We know the estimated population value; it's 50 exactly. So we would expect all our 8 observations to be 50 plus or minus chance error, if we measured without bias. Our mean should be 50.
a. Looking at the table above, it is clear we would use a t-test
b. A plausible hypothesis would be: The reference specimen weighs 50 units.
c. The statistical hypotheses would be:
H0: : obs = 50, the mean of the box we drew our observations from is equal to 50
H1: : obs ¹ 50, the mean of the box we drew our observation from was not 50
d. the df = sample size - 1 or 8 - 1 = 7
e. Let's do the test:
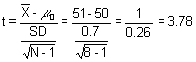
The P value for this comes from the t-table. With 7 degrees of freedom it is less than 0.5% one-tailed. But we have a two-tailed hypothesis, so it is around 1% or so.
f. We reject the null, and conclude that the observations do not seem to come from a reference specimen that really weighs exactly 50 units.