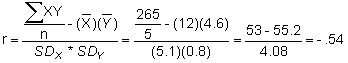Sample Midterm II Questions
a. It can't be this--this is simply the percent of black rabbits I pulled in 100 draws. That's an outcome, not a probability
b. it can't be this--this is the simple probability of 1 draw out of my hat. But I drew 100 times
c. I'm going to have to use z-values to answer this question, and this option shows me a z-value where what I am saying is I pulled 35 black rabbits in 100 draws and I'm contrasting that with my expectation that I should have drawn 100 * .25 or 25 rabbits. I expect there to be some variation around that 25 rabbits simply due to chance so I'm weighting the difference between what I did and what I expect by the expected chance variation (the divisor here). The divisor should be the SE of the total count which is the squareroot of the number of draws times the SD of the box. The square root of 100 is right. And by golly the square root of the probability of pulling a black rabbit * not pulling a black rabbit is the SD of the box. So this option looks correct, but let's check out the last two
d. I may have cheated--you know me--but anything is possible. Even chance alone would allow me to pull 100 black rabbits out of my hat in 100 draws, though it would be very, very, very unlikely that I would ever do that without cheating. Still it is possible.
e. This is a convoluted, and very wrong, z formula. The numerator makes no sense, nor does the denominator.
2. a. The independent variable is the one that we believe influences or causes changes in the other variable. Read the question. You hypothesized that failure to exercise (operationalized here as minutes walking) leads to fatigue. So the independent variable must be minutes walking.
- The correlation between the two can be calculated by either converting all values to z-values and taking the average of the crossproducts:
Score Z Score Z Z*Z
5 (5-12)/5.10= -1.37 5 .5 -0.69
10 -0.39 4 -.75 0.29
20 1.57 4 -.75 -1.18
10 -0.39 6 1.75 -0.68
15 0.59 4 -.75 -0.44
r = (-.69 + .29 - 1.18 -.68 -.44)/5 = -.54
Or by substituting into the formula for the correlation that I gave you:
Score Score Score*Score
5 5 25
10 4 40
20 4 80
10 6 60
15 4 60
sum = 265
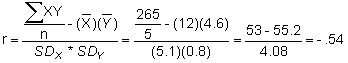
- The more you walk the lower your level of fatigue. Or, there is a negative linear relationship between walking and fatigue such that people who walk more tend to report less fatigue.
3. a. 57%. Knowing nothing other than my sample value, my best guess for the population is my sample. I can't be absolutely certain, nor can I state that it is exactly the same, but it's a better guess than just pulling a number out of my head.
- Well, let's set up the problem
P(For increasing tuition) = 57%
E(X) = 200(.57)= 114 = number of pro votes
SD of the box = (1 -0)* square root of (114/200 * 86/200) = 0.495
SE of the count = square root of (200) * SD of the box = 7.00
SE of the percent = SE of the Count/Number of draws * 100% = 7/200 * 100% = 3.5%
95% CI = 57% plus or minus 2 * 3.5% = an interval of 50% to 64%
- 95% of the time the interval between 50% and 64% will include the population parameter, though we are not certain if this is one of the times when it does not. An approximate 95% confidence interval for the 57% percent observed is 50% to 64%. We cannot say there is a 95% chance the population parameter lies between 50% and 64%. Population parameters are real. There is no chance involved with them--they don't bounce around. Think of it this way, if we flipped a coin and estimated the percentage of time we expect to see a heads happen is there any chance, if the coin is fair, that the probability is not exactly 50%??? Our uncertaintly lies in our estimates not in the population parameter. Our estimates have chance attached to them but population parameters don't.
- Let's set up the box:
2 chances of a vowel -- 1 4 chances of a consonant -- 0
P(vowel) = 2/6 and there are 100 draws
So the E(X) = 100 * 2/6 = 100 *.3333 = 33.33 = the number of draws with vowels we expect to see
The SD of the box = (1 - 0) * square root of (.33 * .67) = 0.47
The SE of the count = square root of (number of draws) * SD of the box = 10 * .47 = 4.70
So we expect to see 33.33 draws with vowels turn up, plus or minus 4.70
We want to know what percent of the time we would actually see 25 or more vowels.
We need to translate this into a z-value to get the percentile
Z = (25 - 33.33)/4.70 = -1.77
This cuts off about (92%/2 + 50% = )96% of the normal curve to the right of the 25 value ("25 or more").