Ó 2004, S. D. Cochran. All rights reserved.

CONFIDENCE INTERVALS CONTINUED
  1. Review of SE's
  1. SD is not SE, though they are both estimates of deviation or variation from the average or an expected value.
  1. SD refers to the spread that we see or observe, either in data we collect or in the values that are possible in the box.

  1. The square of SD is referred to as variance.

  2. Variance is the sum of the squared deviations from the mean.

  3. We use SD to give us a sense of how much spread there is in our sample distribution

  4. The SD tell us how far on average scores are from the average. If we assume normality, if we go out 2 SD to either side of the mean, then approximately 95% of our sample observations are included in that interval

        Example: If I ask each of you how much you like the beach on a 10-point scale, your answers will vary. The numerical center of that variation is the mean, the average spread around that mean is the S.D. The S.D. is caused by true variation, chance, and bias in indeterminable amount
  1. SE refers to the spread that we expect to see due to randomness, that is, it is an estimate of chance, and we use it to estimate the size of chance error.

      Example: If we flip a coin 100 times, we can estimate the average number of heads we would expect to observe if the coin were fair (no bias). The center of that anticipated but not real distribution is the probability of heads occurring and the SE is the spread around the expected value. It is caused by chance alone

  1. The types of SE learned so far
  1. The first SE we learned, SE for the sum of the draws = square root (number of draws) X (SD of the box)

  1. This is an estimate of the spread due to chance around the sum of the draws from the box.

  2. We used this primarily for boxes that were counts (SE for the count). Counts are situations where we want to know the number of times a particular characteristic occurs

  1. SE for probability distributions

  1. Probability distributions, which are theoretical not empirical, have spread also. The distribution is a density function of probability.

  2. Z-scores are an index of SE's for the probability distribution. 1 z = 1 S.E.; -2.3 z = 2.3 S.E.

  1. SE for percentages = (S.E. for the count)/(number of draws) X 100%.

  1. This weights the SE for the sum of draws or the count by the sample size--converts the SE for the count to a percentage of the sample size.

  2. We use SE for percentages to calculate our estimates of chance error in sampling, when our estimate of center is a percentage.

  1. Now we are going to learn a new SE, the SE for the average of draws

  1. This weights the sum of the draws for the sample size or SE for the sum/number of draws.

  2. Notice that this is the same strategy as the SE for percentages.

  3. Here we are trying to estimate the chance spread in our mean, or average of any one draw from the box, when we draw repeated samples from a box that has more than a binomial outcome.

  1. In the SE for percentages we are estimating the chance spread in our count (% of 1’s for example)

  2. In the SE for the average of the draws we are trying to estimate the average value drawn from the box (as opposed to the % of 1’s, let’s say) but the spread is also due to chance error

  1. Central limit theorem

  1. Imagine a situation where we draw 10 independent samples of the same size from the box. Each sample has a mean value. Those 10 means are themselves a sample. They are referred to as the sampling distribution of the means.

  2. Intuitively what might we expect this sampling distribution of the means to look like? Since we are selecting at random from the population we would expect the mean of the distribution of sample means to approximate the mean of the population.

  3. We also might expect that the probability that a sample mean drifts far to one extreme or another is less likely than we would see in the individual values in the original distributions, because means after all are the centers of distributions, so extremes tend to balance each other out.

  4. This is also another way of saying that a sampling distribution of the means should have less variability than a sample distribution.

  5. In fact,

  1. The distribution of sample means from repeated draws of samples of identical size drawn from a population tends to be bell-shaped or normal. Indeed even if the underlying population distribution is skewed or flat or not normal, the distribution of sample means will tend to be normal

  2. The mean of the sample means is expected to be equal to the mean of the population from which the samples were drawn

  3. The distribution of sample means becomes more and more compact as we increase the size of the sampling of samples

  1. These observations illustrate a theorem, the central limit theorem. It states:

    If random samples of a fixed N are drawn from any population (regardless of the form of the population distribution), as N becomes large, the distribution of sample means approaches normality with the overall mean approaching µ, and the standard error,

  1. So what does this mean? We don't ever repeatedly select samples from a population. Instead we select one sample and use that to infer something about the population. The central limit theorem says that we can use our sample mean as an estimate of the population mean. Further, we can, by dividing by the square root of our sample size, use our sample estimate of the standard deviation to estimate the SE of the sampling distribution of the means, 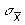. And, because the sampling distribution of the means has a distribution that approximates normal, if the underlying population distribution is normal, we can use the mean and the newly calculated estimate of SE to create confidence intervals.

  2. Remember, the SE tell us the average spread of the sample average in the context of population parameters--for a typical sample. If we go out 2 SE to either side of the sample mean (which is an estimate of the population mean), then 95% of the time we will have created an interval that includes the population mean. That is we can be 95% confident that we will have created an interval that includes the population parameter. Or, to state it another way, we will be correct 95 our of 100 times when we create this type of interval to include the population parameter.