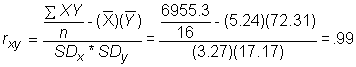- We have learned that a sample distribution has a center,
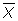 , and a spread, S.D.
, and a spread, S.D.
The S.D. when squared is call the variance
With two variables, each of them separately has a mean and variance in unidimensional space
Ó
2004, S. D. Cochran. All rights reserved.CORRELATION
You do this now intuitively--if you devote all weekend to studying (more numbers of hours) will you do better on your midterms (more points on each exam). This is a positive association--as the values of one variable increase so do the values of the other.
You also might ask a question that reflects a hypothesis about a negative correlation. If I lose weight will I feel more happiness? This is a negative relationship between weight and comfort, because as weight decreases, you hypothesize happiness increases.
Finally, you may also intuitively experience a situation in which two variables are not associated at all. For example, if you think about effort expended as a variable and extent of understanding of a very complicated concept in one of your classes, you might have had the experience that no matter how hard you tried it didn't seem to influence your degree of understanding. This is a situation of no association--and the human emotion attached to that is the perception of helplessness. Statisticians think of it as a lack of covariance.
Example: If I lose weight (weight loss is a causal variable) then I will feel more energy (energy is a consequence)
Variables that we think of as influencing factors are called independent variables
Some independent variables are causal
Some independent variables are not--an example in the book is son's height predicting father's height. Or we might predict height from foot size, but clearly foot size is not causal of height
Variables that we think of as consequential are called dependent variables
Example: If I lose weight (independent variable or IV) then I feel better (dependent variable or DV)
The if-then sentence structure of the logical statement is the clue: If IV then DV.
- We have learned that a sample distribution has a center,
, and a spread, S.D.
The S.D. when squared is call the variance
With two variables, each of them separately has a mean and variance in unidimensional space
Example: We collect data from 16 high school students taking a history class. We ask each of them two questions: how many hours did they study for their last quiz and what was their score. We have to keep track for each subject what his or her two responses were because later we will have to multiply these responses times each other.
The graph showing hours studied has a center and spread. The mean is 5.2 hours, the S.D. is 3.3 hours. Notice that the S.D. is wide in relation to the distribution. Why is that so?
We can also graph the distribution of scores on the quiz. The mean is 72.3 points and the S.D. is 17.2 points.
- We can also plot the joint distribution of the set of scores
In a joint distribution, each observation contains information on two variables. This can be plotted in two dimensions as a point.
Notice that in our example, the joint distribution has the appearance of a line. But it too has a center and a spread. The center is two dimensional, so instead of being a point it is a line, called in the book, the SD line. The spread is the distance points are away from the line or center, vertically.
£ r £ 1, r ranges from -1 to 1
The Pearson r is summary of the extent of association between two variables
Basic facts
-1
When r is 1 or -1, it means that
The joint distribution of x and y forms a straight line, and all the points of the joint distribution are on that line
If we know x and r=1 or r = -1, then we can perfectly predict the value of y
If r is 0, the points of the joint distribution do not form a straight line, but rather a cloud or buck shot. There can also be other shapes which I will get to later.
Pearson r represents the extent to which the same individuals or events occupy the same relative position on two variables.
Another way of stating this is to think of z-scores.
Z-scores are ranks. When we convert a score to a z-score we are ranking that score within the distribution
r calculates the extent to which for two variables, an individual's z-scores, or ranks, are the same
- It is a statement of the direction of association between two variables
When positive, it means as the values of both variable go in the same directions: as one variable increases, so does the value of the other; or as one decreases, the other decreases
When negative, it means that as the values of the two variables go in opposite directions: as one increases, the other decreases
When r is zero exactly, it means that changes in one variable do not predict changes in the other. They are uncorrelated, not associated, independent.
- It is also a statement of the strength of association between x and y
As the spread in the joint distribution away from the line decreases, the size of r increases
This is another way of saying that as r increases, knowing x provides more information about what the value of y might be
- Because a correlation contains two pieces of information it is not enough to say two variables are correlated. You have to convey both pieces of information by saying they are positively correlated or negatively correlated.
- In the book, the calculation involves converting both x and y into standard units and then taking the average of the product of the joint standard scores.
r = (sum (zx)(zy))/(number of elements in the sample)
More typically you will do this automatically in your hand calculator
The formula for r introduces the notion of covariance.
Covariance refers to the extent to which changes in x result in changes in y
There are several formulas for r, all of which are just ways of stating the same thing:
![]()
or a computational formula for raw data:
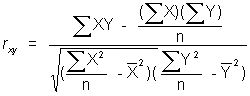
or another computational formula, making use of the mean and standard deviation which we probably have already calculated or may know:
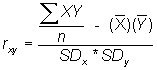
- So, to use our studying and test score data:
- Book method:
Hours
Score
Z(hours)
Z(score
Product
1.2
50
-1.24
-1.30
1.61
1.2
50
-1.24
-1.30
1.61
1.2
51
-1.24
-1.24
1.53
1.7
54
-1.08
-1.07
1.16
2.1
56
-0.96
-0.95
0.91
3.1
62
-0.66
-0.60
0.39
4.0
63
-0.38
-0.54
0.21
4.3
76
-0.29
0.21
-0.06
6.3
74
0.32
0.10
0.03
6.4
80
0.35
0.45
0.16
6.9
80
0.51
0.45
0.23
7.2
82
0.60
0.56
0.34
7.5
83
0.69
0.62
0.43
8.9
93
1.12
1.20
1.35
10.9
101
1.73
1.67
2.89
11.0
102
1.76
1.73
3.04
Sum
83.9
1157
15.81
Mean
5.2
72.3
0.99 = r
(16 elements)
S.D.
3.3
17.2
z for the first element's hours = (1.2 - 5.2)/3.3
- Computational formula method:
|
|
Hours |
Score |
Product |
|
|
1.2 |
50 |
60.0 |
|
|
1.2 |
50 |
60.0 |
|
|
1.2 |
51 |
61.2 |
|
|
1.7 |
54 |
91.8 |
|
|
2.1 |
56 |
117.6 |
|
|
3.1 |
62 |
192.2 |
|
|
4.0 |
63 |
252.0 |
|
|
4.3 |
76 |
326.8 |
|
|
6.3 |
74 |
466.2 |
|
|
6.4 |
80 |
512.0 |
|
|
6.9 |
80 |
552.0 |
|
|
7.2 |
82 |
590.4 |
|
|
7.5 |
83 |
622.5 |
|
|
8.9 |
93 |
827.7 |
|
|
10.9 |
101 |
1100.9 |
|
|
11.0 |
102 |
1122.0 |
|
Sum |
83.9 |
1157 |
6955.3 |
|
Mean |
5.2 |
72.3 |
|
|
S.D. |
3.3 |
17.2 |
|