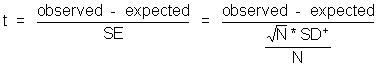
Ó
2004, S. D. Cochran. All rights reserved.T-TESTS
T-tests
With small samples, the distribution of (observed - expected)/SE when the null hypothesis is true does not follow the normal distribution. Instead it follows the t-distribution, which is highly similar, but changes its shape slightly as the sample size increases. Eventually, when the sample size is very large, the t-distribution approaches the normal distribution.
Both distributions are symmetrical about a mean of zero.
The proportion of areas beyond a particular positive t-value is equal to the proportion of area below a corresponding negative t-value, just like the normal distribution
The t-distribution is more spread out than the normal curve. Therefore the proportion of area beyond a specific value of t is greater than the proportion of area beyond the corresponding value of z. The tails are fatter.
The formula for a t-test looks exactly like the z-test except that SE is calculated differently:
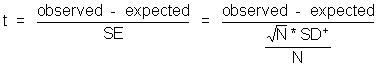
or as you will see presented in other contexts:
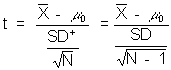
Where do we get the components of this equation?
s mean of X, the small samples underestimate on average the amount of variance, or the size of the standard error of the mean. This is referred as a biased estimate.
Observed refers again to our data--our data provide the mean score for our sample
The expected part refers to our expectations under the null hypothesis, that is the mean of the population when the null hypothesis is true
The SE is still the standard error for the population mean. We do not know it and must estimate it from our sample standard deviation, but now we need to correct for the size of our sample.
When we use small samples to estimate the population parameter,
We want to use an estimate that is unbiased. That is, an estimate which equals, on the average, the value of the parameter. We can do this by adjusting the SD to the sample size. This is referred to in the book as SD+:
![]()
or more formally,
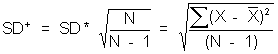
The SD+ is the other standard deviation on your hand calculator, by the way.
The SE is then calculated as before, but this time using the SD+
The S.E. = (square root (sample size) * SD+)/ sample size
or more simply:
The S.E. = S.D./(square root (N - 1))
How do we use the t-test?
The t value that we obtain can be related back to a t-distribution in order to estimate the probability of obtaining a value this far from the population mean or farther.
Unlike a z-test which relates the value obtained to a single normal distribution, the t-test uses a family of t-distributions. We have to relate the t-value obtained to the correct distribution.
Each t-distribution varies depending upon the degrees of freedom.
This refers to the number of values which are free to vary after we have placed certain restrictions on our data
In a one-sample t-test, we use one df to estimate the mean, so our df = N -1
Note that our estimate of the standard error of the population mean is equal to our sample standard deviation divided by the square root of the degrees of freedom.
Using the t-TABLE in the back of the book
Find your df, which is the sample size minus one
Choose your desired P value, commonly 5% for a one tailed test, 2.5% for a two-tailed test
Find the critical value of t.
Is your calculated t-value equal to or greater than the critical value of t?
If not, you do not reject the null hypothesis
If yes, you do REJECT the null hypothesis
Example
Let's say a group of 17 average ninth grade students are assigned to a new style of science teaching. Their performance before entering the new classroom was average, though as a result of the new style of classroom instruction we believe they should score higher than average on tests of science knowledge if the new curriculum is working. After 6 weeks in the classroom, we give them a test assessing their knowledge of basic science concepts to see if the teaching has been effective. We find the following:
= 84, S.D. = 16, N = 17
We know from studies done at UCLA that ninth graders in general score an average of 78 on this exam (µ0 = 78). Is the difference we observed after six weeks of instruction consistent with what is likely under conditions of chance alone of does it reflect a true difference, a better performance on the test than average?
What is our research hypothesis?
The new teaching style resulted in a better test performance than average ninth graders.
We need two mutually exclusive and exhaustive statistically hypotheses:
Our sample does not differ in knowledge of science concepts from average 9th graders. The null hypothesis is:
H0: µ1 = µ0
Our 9th graders score differently than other 9th graders--the alternative hypothesis
H1: µ1 ¹ µ1
Notice that this alternative allows for the possibility that the new teaching style actually harmed these students. This hypothesis is two-tailed.
We choose to use a t-test instead of z-test because we have a small sample. We set our desired level of statistical significance or alpha at P = .05, cutting off 2.5% of the distribution in each tail.
The SE is derived from the SD+
The SD = 16
The SD+ = square root (17/(17 - 1)) * 16 = 1.03 * 16 = 16.49
The SE for the sum = square root (17) * 16.49 = 4.12 * 16.49 = 67.99
The SE for the average = 67.99/17 = 4.00
We could also do it directly from the alternative formula:
S.E. = S.D./(square root (N - 1)) = 16/square root (16) = 4
So t = (84 - 78)/4 = 6/4 = 1.5
Our df = n - 1 = 17 - 1 = 16.
Looking in the t-TABLE, with df = 16, we need an obtained t-value of 2.12 to reject our null hypothesis.
We therefore FAIL TO REJECT our null hypothesis, and conclude there is no evidence in our study that these students' higher scores on the test are due to anything other than chance variation
This does not mean that the null hypothesis is correct and the alternative incorrect. It could be that the difference is due to improvements from the new teaching style. But our result is not strong enough for us to see it unequivocally. You can never be absolutely certain.
When do we use a t-test or a z-test?
We use a z-test if our sample is very large, such as greater than a couple of hundred subjects.
When our sample is small, we still use a z-test if our estimate of the S.E. of the population mean is a known parameter.
Example: I.Q. tests are typically standardized with a mean of 100 and a SE of 15. These are based on the population.
However, when our sample is small, and the SE of population mean must be estimated from our sample statistics, we use a t-test
There are three common types of t-tests. We have just learned the one-sample t-test. There is also a two-sample t-test. And a paired-t-test used when we measure, for example, the same person twice and want to compare his or her two scores.