Ó
2004, S. D. Cochran. All rights reserved.TWO SAMPLE Z-TESTS
So far, we have learned to test hypotheses involving one sample, where we contrasted what we observed with what we expected from the population. Often times, scientists are faced with hypotheses about differences between groups.
Examples: What is the effect of taking a drug vs. a placebo in controlling pain? Do interest rates rise more quickly when wages increase or stay the same? Who is more likely to vote in an election, Democrats or Republicans? Each of these involves comparison of at least two samples.
It is easy here to get confused: in the case of differences between groups, we may literally draw one sample, but because we consider the sample as two separate and independent groups, we call the statistical tests two-sample tests.
Example: We might want to compare the number of pizza slices eaten by male and female college students. We randomly select a sample of students, of whom some are male and some are female. Although we have one sample; we also think of it as two independent samples that just happened to be selected at the same time.
In the book, the authors show this for the case of an experiment when there is random assignment. They show a box model where on the ticket for each subject is their response under treatment A and their response under treatment B, where only one of these two possibilities is observed in the study.
The same can be thought of for our example. Each person has a ticket. On the ticket is the number of pizza slices they would eat if they were male and if they were female. Obviously one of the possibilities cannot occur in reality. It is fixed before the researcher draws the sample. This is another way of saying that if we compare men and women, it is not an experiment, but an observational study.
When testing for the differences between two groups, we can imagine two separate situations.
¹ 0, or alternatively, µ1 ¹ µ2
In one, there is no real difference between the two groups.
This can occur if there is simply one population, and we randomly select two samples from it. On average, we would expect the means of these two samples to be identical, except for chance variation. The expected difference between the two means would be zero. Example: we randomly select two samples from a population and subject one, but not other, to a treatment that does not change it in any way. The samples are still from the same population and return unchanged to the same population.
This can also occur when two populations may perfectly overlap. Example: Situations where there are no sex differences in performance. The populations are separate but overlapping.
When we expect there to be no differences between the two groups, this is generally the null hypothesis. The null states that the population means of the two groups are identical, so their difference is zero.
Formally, H0: µ1 - µ2 = 0, or alternatively, µ1 = µ2
In the other situation, the mean difference between the two groups is not zero.
This means that the two groups are different in their true scores--that it is not just chance variation that results in the observed means not being precisely identical
Generally this is the alternative hypothesis, and it states that the means are not the same
Formally, H1: µ1 - µ2
When we sample two independent quantities, the standard error for the difference is:
![]()
This is our estimate of the average size of chance error we expect to observe when we sample twice either from the same population or two populations that do not differ.
[The reason for this:
Think of a linear combination of J random variables: Y = c1X1 + ... + cjXj
In the special case, given n sample values drawn from the same distribution with mean,
m , then the expected value of any linear combination of those sample values is:E(y) =
m (c1 + ... + cn)and the variance is the sum of all individual variances times their squared weight + 2 times the sum of their covariances. In this instance we assume that they are independently drawn, and so the covariances are zero resulting in:
![]()
]
We can use the two-sample z-test to evaluate the difference between two groups:
![]()
or more formally:
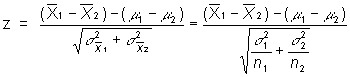
Where do we get the components?
The observed difference refers to the difference between the means of two groups
The expected difference, generally, under the null hypothesis is 0, so this drops out of the equation
The SE for the difference is:
![]()
From the SD of each sample, calculate the SE for the sum
SE for the sum of group 1 = square root (sample size of group 1) * SD of group 1
SE for the sum of group 2 = square root (sample size of group 1) * SD of group 1
Then calculate the SE for the average
SE for the average of group 1 = SE for the sum/sample size of group 1
SE for the average of group 2 = SE for the sum/sample size of group 2
Then square each of these, sum them, and take the square root
Alternatively, we can calculate this directly from the formal equation using the SD, or s, and the sample sizes:

Example
Imagine a researcher wants to determine whether or not a given drug has any effect on the scores of human subjects performing a task of ESP sensitivity. He randomly assigns his subjects to one of two groups. Nine hundred subjects in group 1 (the experimental group) receive an oral administration of the drug prior to testing. In contrast, 1000 subjects in group 2 (control group) receive a placebo.
What is our research hypothesis?
Taking this drug changes performance on a task of ESP sensitivity.
Now we need to translate the research hypothesis into a testable statistical hypothesis
The null hypothesis (H0): There is no difference between the population means of the drug group and no-drug group on the test of ESP sensitivity, that is H0: µ1 - µ2 = 0
This means essentially that the two populations are identical in ESP sensitivity after administration of the drug. Because our research hypothesis is that they should differ, this is the logical alternative, and in fact the only hypothesis we can evaluate. If it is not likely to be true, then indirectly we have evidence supporting our alternative hypothesis.
¹ 0
The alternative hypothesis (H1): There is a difference between the population means of the drug group and no-drug group on the test of ESP sensitivity, that is H1: µ1 - µ2
Notice this is our research hypothesis in statistical form. It exists, but we never directly evaluate its plausibility.
The results of the study found the following:
For the drug group, the mean score on the ESP test was 9.78, S.D. = 4.05, n = 900
For the no-drug group, the mean = 15.10, S.D. = 4.28, n= 1000
So, under the null hypothesis:
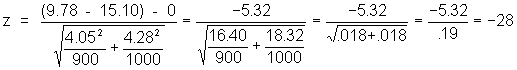
or, doing it by the book:
The SE for the sum of group 1 = square root (900) * 4.05 = 30 * 4.05 = 121.5
The SE for the sum of group 2 = square root (1000) * 4.28 = 31.62 * 4.28 = 135.34
The SE for the average of group 1 = 121.5/900 = .135
The SE for the average of group 2 = 135.34/1000 = .135
So the SE for the difference = square root (.1352 + .1352) = .19
z = -5.32/.19 = -28
The P associated with a difference this strong or stronger is extremely rare, so we REJECT the plausibility of our null hypothesis.
We therefore accept the alternative, and conclude that in fact there is a difference between the two groups. But wait a minute, the group that got the drug did worse than the control group. We know this from the negative sign of the difference between the two means. It appears the drug hampers ESP ability. Remember that even when we reject the null hypothesis, we have to be cognizant of the sign of the Z-test, or the original means of the two groups, to make a conclusion about the direction of the difference.
In actuality, two sample z-tests are rarely used, because the estimate for the SE for difference used here is biased. Instead, statisticians use a two-sample t-test. But that is beyond this course. However, the methods and equations are very similar to what we learned with the z-tests and the one-sample t-test.