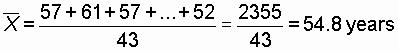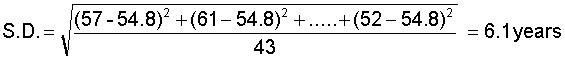SUMMARIZING DATA NUMERICALLY  

1. In this next section we are going to learn how summarize data by calculating an estimate of the average value in a distribution and an estimate of how much the values in the distribution cluster around that average.
   
2. What is meant by average? There are three ways of defining average. 

So the modal student in this class is a sophomore. That is the year in school that is most commonly represented in this class is a sophomore. 

But the mode tells us nothing about the rest of the distribution. For example, it does not tell us whether sophomores make up most of the class, that is more than 50%, or get their label as modal because they just squeak by the rest at 26%. 

Example: Imagine the following ages of 6 children: 6, 5, 7, 6, 6, 5. The modal age is 6. It is the most common age among the children. 

2. A second way of thinking about average is to look at what is the middle of the distribution. This is called the median. The median is that point at which 50% of the distribution lies above and 50% lies below. 

Example: In a second group of 6 children there were the following ages: 5, 9, 11, 6, 3, 1. If we arrange the ages in numerical order we can see that half are 5 and below; half are 6 and above so the median age is 5.5 years 

The median gives us a clear sense of the middle of the distribution but often times it is a general sense rather than a precise sense.  

3. A third way of thinking about average is the mean. The mean is a weighted sum. We calculate it by summing all the scores and then weighting by the number of scores that contributed to that sum. In that way we control for the size of the sample that contributed scores.  

For example, if we sampled 3000 students or 300 students from UCLA and asked how frequently they exercised, the mean would be very close to the same, because by dividing by the sample size we adjust or weight for that factor. 

The mathematical formula for the mean is: given a list of n numbers, 

 

Example: In our first group of children the mean is (6+ 5+7+6+6+5)/6=5.83 

4. Some final thoughts about the averages

1. The mean is the balancing point of a distribution, which is something covered extensively in the chapter
2. If the distribution is symmetric, the mean is equal to the median
3. The mean is sensitive to extreme values, so if you have a distribution with a long tail to one side, the mean is drawn toward that tail--if the long tail is on the right the distribution is said to be positively skewed; if the long tail is on the left so that many values exist at higher numbers then the distribution is negatively skewed (drawn in the negative direction)--in this case it might be more appropriate to report the median 
4. Most of you have an intuitive sense of the mean. You can look at two different distributions and know right off that their mean is different. 

Example: In one of our groups of children the ages were 6, 5, 7, 6, 6, 5. If we had a group of adults with the following ages: 42, 45, 51, 60, 48, do you need to calculate a mean to know that the means are different? Does it matter that one group has 6 elements and one has 5? 

The next concept you don't have that intuitive feel for yet, but with practice you will. 

C. Measuring spread 

1. A second way of describing a distribution is to quantify the average spread away from the center of a distribution 

2. The first step in measuring spread of a distribution is to have in the mind the concept of distance. How far from average are people on average? If everyone is average exactly then nobody differs from average, which is another of saying that everybody is exactly the same and there is no distance between them.  
   
3. One way of beginning to quantify distance is the root-mean-square approach 

4. But what we would really like to know is how far on average is a score from average. To do this we have to calculate the standard deviation. This is abbreviated as S.D., or on many calculators as "s" or "s " (sigma).

1. One component of the standard deviation, is the deviation from the average. That is how far is a score from the mean. This is simply:

7. What is the advantage of knowing the S.D.? As we will learn in the next lecture, one S.D. to the right and left of a mean includes about 68% of a distribution--not always exactly, but generally in the ballpark. Two S.D.'s cuts off about 95% of the distribution. 

4. Let's go through a real example. Imagine a distribution of U.S. President's ages at the time they are inaugurated. We want to be able to summarize this data in a way where we can give other people a sense of how old are U.S. President's when they take office. 

1. We could list every element, that is every President, and let people make their own summary judgment, so I might show you the following list of numbers: 

2. We could do some of the summary work and make a histogram of their ages 

3. But, we could say most of what we need to know about this distribution in only 2 numbers. That is we could answer those two questions I asked by knowing just 2 numbers. The first is the average and second is the spread.
   
4. We know there are 3 types of averages 

1. The mode or most common element in the distribution. In the president's age raw data the mode is 51. Five men were 51 years old when they took office. No other age was represented this frequently 
    
2. The median is that point in the distribution that 50% of the ages lie above and below it. In our president's age raw data, the median is 55 years. That is around 50% of men were 55 years or younger when they took office (57%). But you can see here the problem with median. It is also true that around 52% of presidents were 55 years or older when they took office. We could calculate an age within that one year interval to state median more precisely. 
   
3. The mean, or numerical midpoint in the distribution. We can calculate the mean of the presidents' age distribution, and we find the following: 

5. We can also calculate the average spread around that central point. It is simply the r.m.s of the deviations from the mean. So, in our Presidents' age data, it would be 

6. Knowing these two facts, the average and average spread away from average, I can dazzle you with seemingly awesome predictive powers.