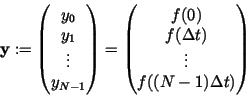
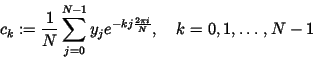
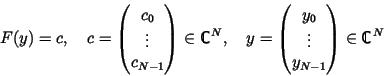
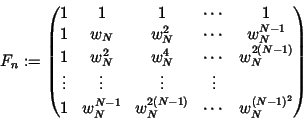
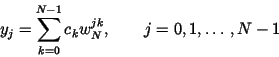 |
(15) |
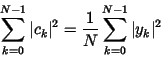
We divide c in its odd and even indices
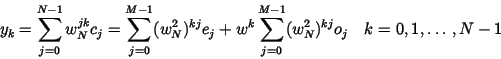
y is splitted in
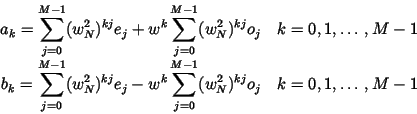
In order to perform a Fourier transform of length N, one need to do two Fourier transforms FM e and FM o of length M on the even and odd elements. We now have two transforms which take less time to work out. The two sub-transforms can then be combined with the appropriate factor wk to give the IDFT. Applying this recursively leads to the algorithm of the Fast Fourier transform (FFT).
/*
x and y are real and imaginary arrays of 2^m points.
dir = 1 gives forward transform
dir = -1 gives reverse transform
*/
FFT(int dir, int m, double *x, double *y)
{
int n,i,i1,j,k,i2,l,l1,l2;
double c1,c2,tx,ty,t1,t2,u1,u2,z;
/* Number of points */
n = 1;
for (i=0;i<m;i++)
n *= 2;
/* Bit reversal */
i2 = n >> 1;
j = 0;
for (i=0;i < n-1; i++) {
if (i < j) {
tx = x[i];
ty = y[i];
x[i] = x[j];
y[i] = y[j];
x[j] = tx;
y[j] = ty;
}
k = i2;
while (k <= j) {
j -= k;
k >>= 1;
}
j += k;
}
for (i=0;i < n; i++) {
printf("x[%i] = %f y[%i] = %f\n", i, x[i], i, y[i]);
}
printf("-------------------------\n");
/* compute the FFT */
c1 = -1.0;
c2 = 0.0;
l2 = 1;
for (l=0;l<m;l++) {
l1 = l2;
l2 <<= 1;
u1 = 1.0;
u2 = 0.0;
for (j=0;j<l1;j++) {
for (i=j;i<n;i+=l2) {
i1 = i + l1;
t1 = u1 * x[i1] - u2 * y[i1];
t2 = u1 * y[i1] + u2 * x[i1];
x[i1] = x[i] - t1;
y[i1] = y[i] -t2;
x[i] += t1;
y[i] += t2;
}
z = u1 * c1 -u2 * c2;
u2 = u1 * c2 + u2 * c1;
u1 = z;
}
c2 = sqrt((1.0 - c1) / 2.0);
if (dir == 1)
c2 = -c2;
c1 = sqrt((1.0 + c1) / 2.0);
}
/* scaling for forward transform */
if (dir == 1) {
for (i=0;i<n;i++) {
x[i] /= n;
y[i] /= n;
}
}
}
Developed by Marian Prutscher: Email