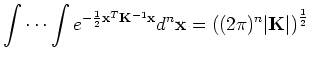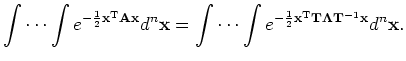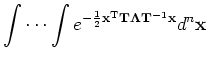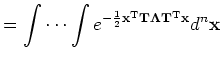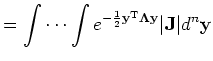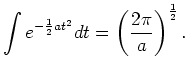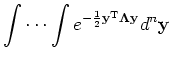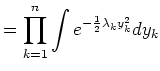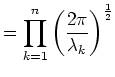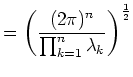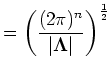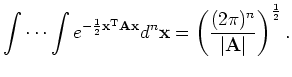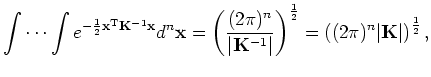Ivo Dinov
UCLA Statistics, Neurology, LONI

Courses	SOCR	Ivo Dinov's Home
SiteMap	Software	Contact

Multidimensional Normal (Gaussian) Distribution

Centralized (unnormalized) multidimensional Normal (Gaussian) distribution is denoted by: N(0, K) where the mean is 0 (zero) and the covariance matrix is K = ( K_i,j ) = Cov(X_i, X_j) . K is symmetric by the identity, i.e., Cov(X_i, X_j) = Cov(X_j , X_i) . Let X = [X₁, X₂, X₃, ...X_n]^T and n-dimensional derivatives are written as $d^n \mathbf{x} \equiv \prod_{i=1}^{n} d x_n$ .

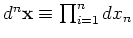The density function of N(0, K) is exp ( -1/2 X^T K^-1 X ), normalizing constant of the N(0, K) density is:

$\displaystyle \idotsint e^{-\frac{1}{2} \mathbf{x}^T \mathbf{K}^{-1} \mathbf{x}} d^n \mathbf{x} = \left((2\pi)^n \vert\mathbf{K}\vert \right)^{\frac{1}{2}}$

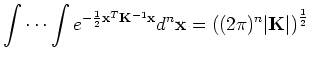(1)

where |K| = det( K ) is the determinant. In general, if multidimensional Gaussian is not centered then the (possibly offset) density has the form: exp [ -1/2 (X-μ)^T K^-1 (X-μ) ].

Because K^-1 is real and symmetric (since (K^-1)^T = (K^T)^-1 ), if A = K we can decompose A into A = T Λ T^-1, where T is an orthonormal matrix ( T^T T = I ) of the eigenvectors of A and Λ is a diagonal matrix of the eigenvalues of A. Then the multidimensional Gaussian density can be expressed as:

$\displaystyle \idotsint e^{-\frac{1}{2} \mathbf{x}^{\mathrm{T}} \mathbf{A} \mat... ...hrm{T}} \mathbf{T} \mathbf{\Lambda} \mathbf{T}^{-1} \mathbf{x}} d^n \mathbf{x}.$

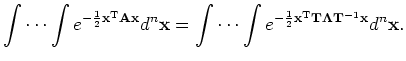(2)

However, T is orthonormal and we have T^-1 = T^T . Now define a new vector variable Y = T^T X, and substitute in (2):

$\displaystyle \idotsint e^{-\frac{1}{2} \mathbf{x}^{\mathrm{T}} \mathbf{T} \mathbf{\Lambda} \mathbf{T}^{-1} \mathbf{x}} d^n \mathbf{x}$	$\displaystyle = \idotsint e^{-\frac{1}{2} \mathbf{x}^{\mathrm{T}} \mathbf{T} \mathbf{\Lambda} \mathbf{T}^{\mathrm{T}} \mathbf{x}} d^n \mathbf{x}$	(3)
	$\displaystyle = \idotsint e^{-\frac{1}{2} \mathbf{y}^{\mathrm{T}} \mathbf{\Lambda}\mathbf{y}} \vert\mathbf{J}\vert d^n \mathbf{y}$	(4)

where | J | is the determinant of the Jacobian matrix J = ( J_m,n ) = ( ∂X_m / ∂Y_n). As X = (T^T)^-1Y = Y , J ≡ T and thus | J | = 1.

Because Λ is diagonal, the integral (4) may be separated into the product of n independent Gaussians, each of which we can integrate separately using the 1D Gaussian:

$\displaystyle \int e^{-\frac{1}{2} a t^2} dt = \left(\frac{2 \pi}{a}\right)^{\frac{1}{2}}.$

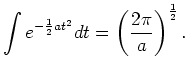(5)

Summarizing:

$\displaystyle \idotsint e^{-\frac{1}{2} \mathbf{y}^{\mathrm{T}} \mathbf{\Lambda}\mathbf{y}} d^n \mathbf{y}$	$\displaystyle = \prod_{k=1}^{n} \int e^{-\frac{1}{2} \lambda_k y_k^2} d y_k$	(6)
	$\displaystyle = \prod_{k=1}^{n} \left(\frac{2 \pi}{\lambda_k}\right)^{\frac{1}{2}}$	(7)
	$\displaystyle = \left(\frac{(2 \pi)^n}{\prod_{k=1}^{n}\lambda_k}\right)^{\frac{1}{2}}$	(8)
	$\displaystyle = \left(\frac{(2 \pi)^n}{\vert\mathbf{\Lambda}\vert}\right)^{\frac{1}{2}}$	(9)

Orthonormal matrix multiplication does not change the determinant, so we have

| A | = | T Λ T^-1| = | T | | Λ | | T^-1| = | Λ |

And therefore:

$\displaystyle \idotsint e^{-\frac{1}{2} \mathbf{x}^{\mathrm{T}} \mathbf{A} \mat... ...\mathbf{x} = \left(\frac{(2 \pi)^n}{\vert\mathbf{A}\vert}\right)^{\frac{1}{2}}.$

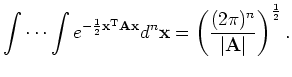(10)

Substituting back in for K^-1 ( A = K and | K^-1 | = 1 / |K| ), we get

$\displaystyle \idotsint e^{-\frac{1}{2} \mathbf{x}^{\mathrm{T}} \mathbf{K}^{-1}... ...ght)^{\frac{1}{2}} = \left((2 \pi)^n \vert\mathbf{K}\vert\right)^{\frac{1}{2}},$

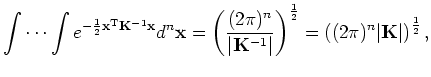(11)

as we expected.

Ivo Dinov's Home

http://www.stat.ucla.edu/~dinov

Visitor number

, since Jan. 01, 2002

_{Last modified
on

GMT by}