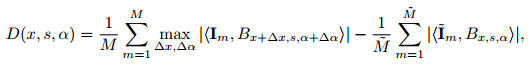
To compare the generative boosting algorithm with the two-stage algorithm based on shared matching pursuit, we conduct two experiments that compare the two methods using two criteria.
We define
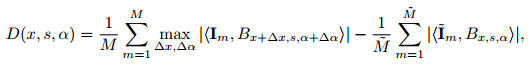
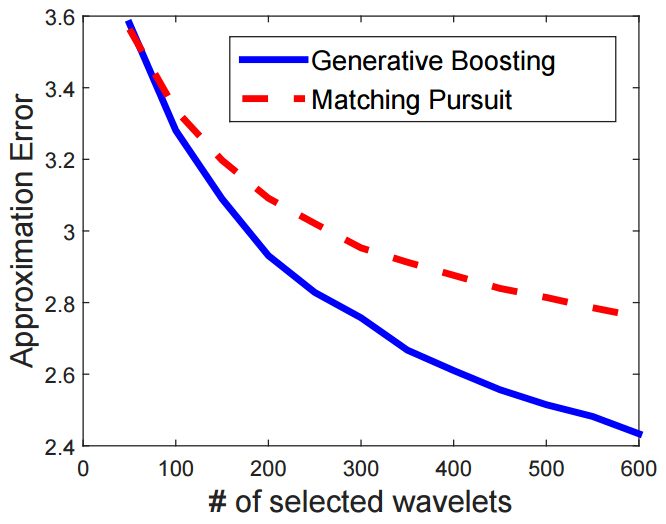
The quantity D(x, s, α) measures the discrepancy between the fitted model and the observed data as far as the wavelet Bx,s,α is concerned. We can compute the average of |D(x, s, α)| over all x, s, α as an overall measure of discrepancy or approximation error. The following figure plots the approximation error versus the number of wavelets selected for the generative boosting method and the shared matching pursuit method respectively for learning from the cat images. It can be seen that generative boosting leads to a faster reduction of the approximation error.
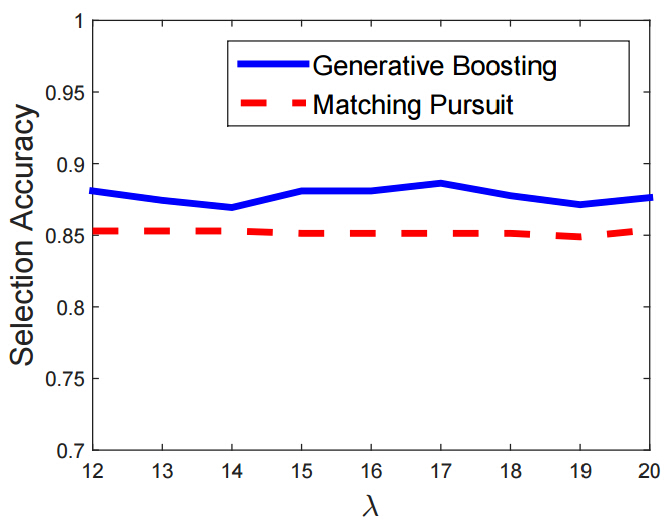
In this experiment, we use a pre-defined model with known B = (Bi = Bxi,si,αi , i = 1, ..., n) and λ = (λi , i = 1, ..., n) as the true model to generate training images so that we know the ground truth. The pre-defined model has the shape of a square, and we allow some overlap between the wavelets Bi that make up the shape of the square. We use n = 16 wavelets in this experiment, and we generate M = 36 training images, assuming that all λi are equal for simplicity. Let B' = (B'i, i = 1, ..., n) be the selected wavelets learned from the training images, where n is assumed known. We use the correlation between Σni=1 Bi and Σni=1 B'i as the measure of accuracy of recovering the true wavelets.
The follwoing Figure plots the selection accuracy versus typical values of λi for generative boosting and shared matching pursuit. The accuracy is computed by averaging over 10 repetitions. It can be seen that generative boosting is consistently more accurate than shared matching pursuit. In this experiment, we use the Gibbs sampling of filter responses, and the wavelet selection is based on the noiseless synthesized images. Before selecting each new wavelet, we estimate the parameters of the current model by maximum likelihood.