iFRAME (inhomogeneous Filters Random Field And Maximum Entropy)

Experiment 7: Mixing of sampling

Code and dataset

Experiment description

We evaluate the mixing of the Gibbs sampling on wavelet coefficients by running parallel chains that sample from the fitted sparse FRAME model p(I; B, λ), where B={B_i, i=1,...,n} are the selected wavelets. These chains start from independent white noise images. Let be the image of chain m produced at iteration t, where each iteration is a sweep of the Gibbs sampler with random scan. Let r_m,t,i =<, B_i> be the response of the synthesized image to B_i. 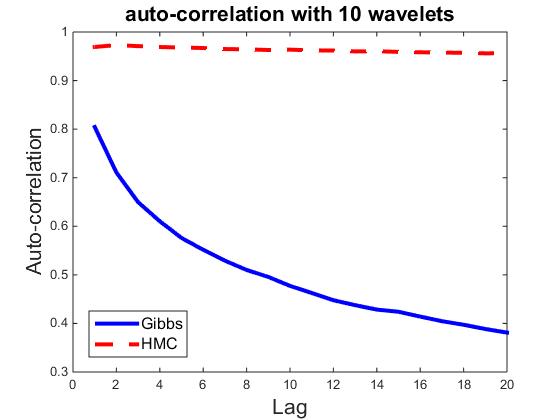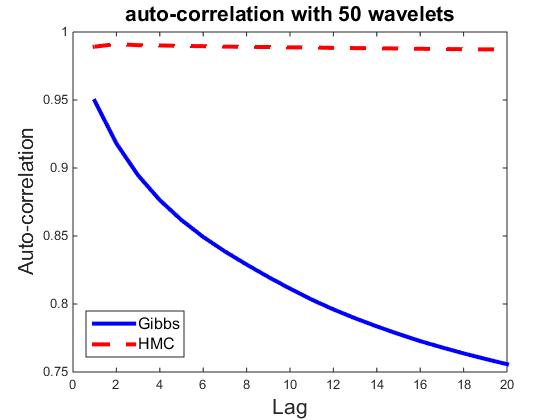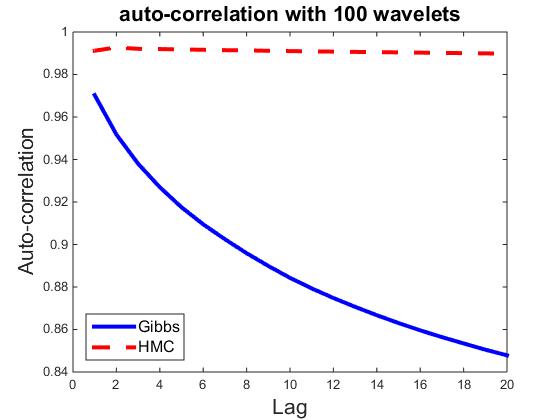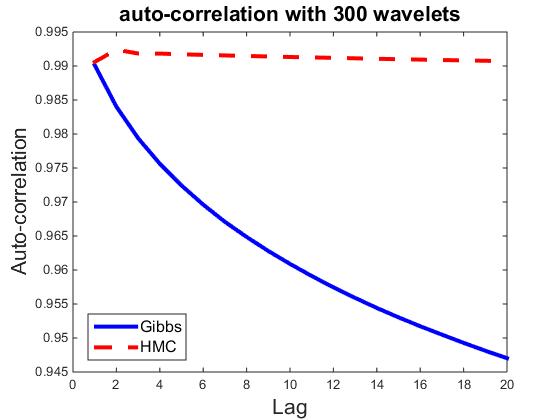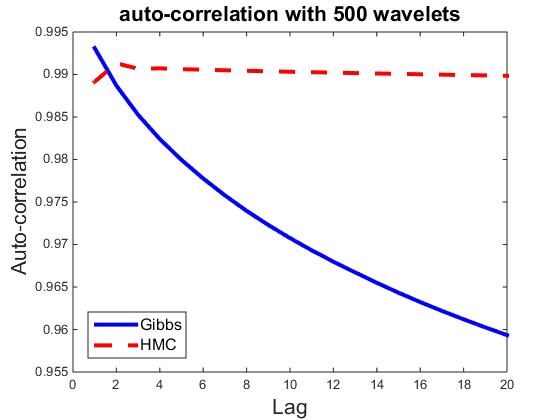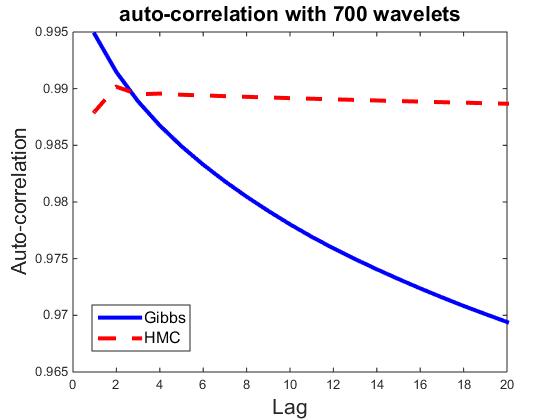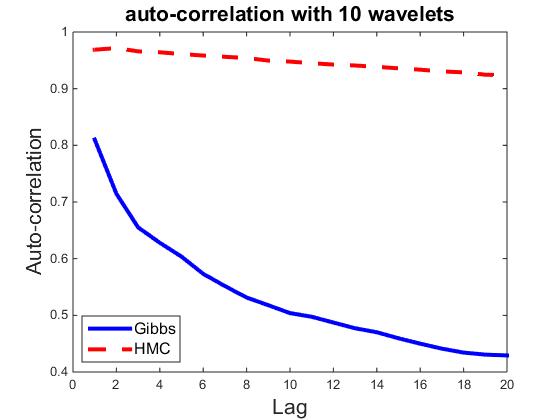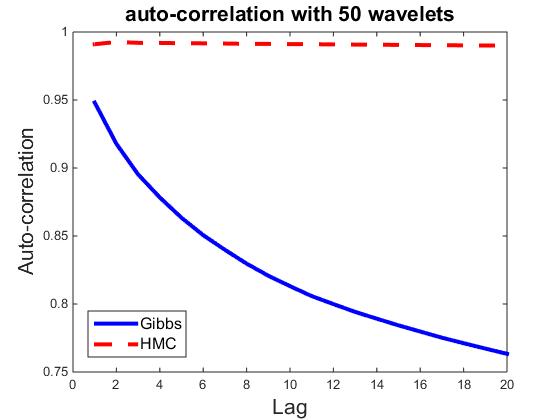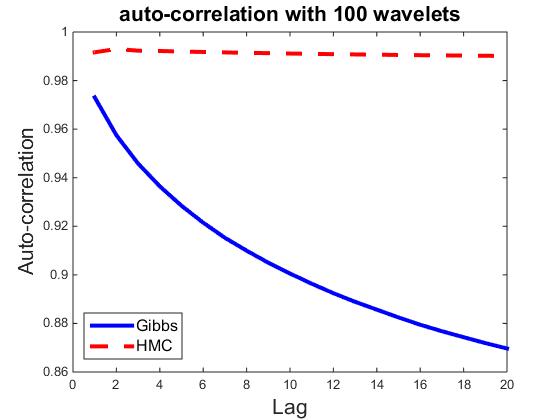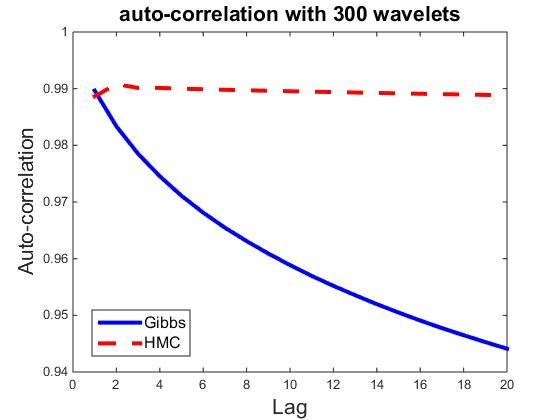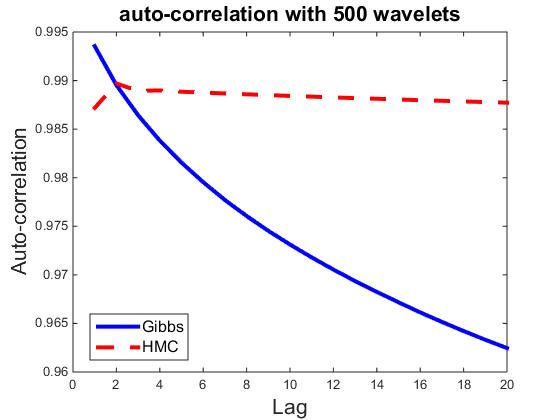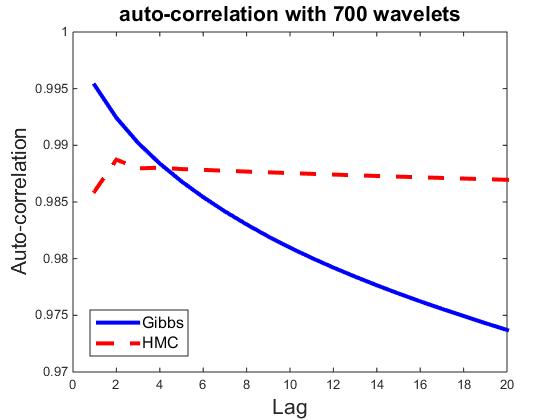Let R_t,i=( r_m,t,i, m=1,...,) be the dimensional vector. Fix t = 100, let ρ_k,i be the correlation between vectors R_t,i and R_t+k,i Then ρ_k=∑ⁿ_i=1 ρ_k,i/n measures the average auto-correlation of lag k, and is an indicator of how well the parallel chains are mixing. As a comparison, we also compute ρ_k for HMC sampler, where each iteration consists of 30 leapfrog steps. Figures plot ρ_k for k = 1,...,20, and for n = 10, 50, 100, 300, 500, and 700, where each plot corresponds a particular n. It seems that HMC can be easily trapped in the local modes, whereas the Gibbs sampler is less prone to local modes.

Case 1: Tiger

Case 2: Cat