This is pulled off of old exams for classes that used a different textbook. So this might not be representative of what you will see for your midterm. In particular, you can expect questions about the 5-step process.
1. The bite of a type of fly that lives in Brazil causes lesions on the skins of those bitten. To measure the size of the lesions, physicians give the bite-victims something called a Montenegro (MTN) Skin Test; a small injection of a substance that causes a splotch to appear on the skin. The area of this splotch is proportional to the area of the lesions. Therefore, by measuring the area of the Montenegro skin test splotch, they can measure the area of the lesions.
b) (5) In order to estimate the mean area of the
MTN skin test, a random sample of 35 fly-bite victims was collected. Here
is a summary of the MTN areas (in square millimeters). Find a 90% confidence
interval for the mean MTN area.
| Variable | N | Average | Std. Dev | Minimum | Median | Maximum |
| mtn | 35 | 34.514 | 24.057 | 9 | 33. | 120. |
The question should have said to find an approximate 90%
confidence interval, because we cannot find an exact CI without assuming
that the distribution of areas
is normal. Without this assumption, the best we
can do here is call on the Central Limit Theorem and hope that the sample
size is sufficiently large to provide a normal sampling distribution, even
if the population distribution is not normal.
Because the SD of the population is unknown, we use the estimated value from this sample: 24.057. This means we use the t-distribution with n-1 = 34 degrees of freedom.
the formula is now Xbar +- t* s/sqrt(n) where t* is the value that has area alpha/2 above it in a t distribution with 34 degrees of freedom.
For a 90% CI, alpha = 10%, so we want the point that "cuts off" an area of 5% in each tail. We could get this from Table F in the book, but this table stops at 29 degrees of freedom (the next step is "infinity"). The difference between using 29 degrees of freedom and infinity is only .06, so it doesn't make too much difference. But to error on the side of caution, lets make the CI too wide and choose 1.31 as our t* value.
34.514 +- 1.70*(24.057/sqrt(35)
34.514 +- 6.913 (6.913 is the "margin of
error".)
(27.601, 41.427) is the approximate 90% CI for
the population mean.
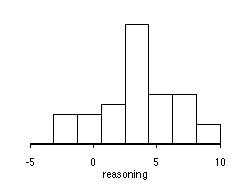
2. Do piano lessons improve the spatial-temporal reasoning of preschool children? Neurobiological arguments suggest that this may be true. A study designed to test this hypothesis measured the spatial-temporal reasoning of 34 preschool children before and after six months of piano lessons. The changes in the reasoning scores are summarized below. (Change is measured as the After score minus the Before score.)
Variable N Average Std. Dev Minimum Median Maximum
reasoning 34 3.6176 3.0552 -3. 4. 9.

Is there evidence that piano lessons improve the spatial-temporal reasoning of preschool children? To answer this question, do the following:
a) Find a 95% confidence interval for the mean change
in reasoning scores.
Here the shape of the distribution of the sample -- unimodal
and more-or-less symmetric -- suggests that the distribution of the population
is likely to be unimodal and symmetric, too. This means that the
CLT is likely to be a good approximation. Again, the SD of the population
is not known, so we rely on the t-distribution.
3.6176 +- t* 3.0552/sqrt(34)
where t* is the value on a t-distribution with 33 degrees
of freedom (n-1) that has an area alpha/2 = .05/2 = .025 above it.
AGain, Table F doesn't have this, but we can conservatively choose the
value for 29 degrees of freedom: 2.05.
CI is 3.6176 +- 1.074
(2.54, 4.692)
b) State the assumptions you made to get this confidence
interval. Do you think the assumptions are good? Based on what evidence?
We assumed that the population distribution is symmetric
and unimodal, which, given the shape of the histogram, is probably a good
assumption. If we want to assume the distribution is normal, then
our confidence interval is exact (although we did have to use 29 degrees
of freedom rather than 33, but other than that, it would be exact.)
Even the assumption of normality is not too far fetched, since the histogram
looks like it could have plausibly come from a normal population. (But
in later statistics classes you'll talk about how to test this a little
more carefully.)
c) Is your confidence interval evidence that spatial-temporal
reasoning was improved by piano lessons? Explain.
Yes. The true mean improvement is either in this
interval or not. 95% of all CIs computed using a study like this
one would cover the true value, so there is only a 5% that our study produced
a CI that does not contain the true value. Notice that 0 or negative
values are NOT in the interval, so we can be pretty confident that the
mean improvement is a positive value: which means that on average people
improved.
3. (5) In the last problem, suppose that you had found that there was a significant change in reasoning scores. Can you conclude that the change was due to piano lessons? If yes, explain why. If no, explain how you would design a study that would allow you to conclude that piano lessons caused the change.
No, you can't conclude that the piano lessons were to blame because there is no control group. Perhaps all children improve their reasoning scores after 6 months, whether or not they take piano lessons. To improve this study, we should randomly assign some children to some sort of "control" activity that does not involve music lessons.
4. An airline knows, through experience, than 10% of the passengers with tickets will not show up for their flight. For this reason, it overbooks flights. For a plane with 100 seats, it will sell 105 tickets. Assume that all ticketed passengers are flying alone and make their decisions about showing up without consulting each other.
a) (5) Let X represent the number of people out of 105 who show up for their flight . What is the distribution of X and why?
X follows a binomial distribution with n = 105 and p = .90. Why? X is the number of successes in a fixed number (105) of trials. Each trial is either a success (shows up) or failure (doesn't show up). The probabilty of success is the same (90%) for each trial. We can assume that outcomes are independent, which might not be a good assumption for people traveling together. None-the-less, without any other evidence and for the sake of getting at least an approximate answer, we make this assumption. Possible values for X are 0,1,2,...,105
b) (5) What's the probability all 105 passengers will show up? (Don't give a number -- just a formula.)
Because outcomes are independent, P(all 105 show up) = P(passenger #1 shows up AND passg. #2 AND....AND passg. #105) = P(Psg #1)*P(psg. #2)*..*P(psg. # 105) = .9^(105) (.9 raised to the 105th power.) This is about 1.6X10^-5 in case you were wondering.
c) (5) Use the normal approximation to find the probability that there will be angry passengers who do not get a seat on the plane.
X is really binomial with n = 105 p = .9. This means
E(X) = np = 105*.9 = 94.5. And SD(X) = sqrt(np(1-p)) = 3.074.
Because np > 10 and n(1-p) > 10 (just barely!), the normal
approximation should be fairly good. So we can "pretend" that
X is N(94.5, 3.074)
P(X > 100) = P(Z > (100 -94.5)/3.074) = P(Z > 1.789)
where Z is a standard normal RV. Using Table E, we find
P(Z > 1.79) = 1 - P(Z <= 1.79) = 1 - .9633 = .037
so there is a 3.7% chance that too many passengers will
show up.
5. A well known scientific theory states that the rate of coughs at a symphony concert during flu season is lambda=2.5 per minute. Let X represent the number of coughs in a one minute period during a flu-season symphony concert. Suppose that X follows a Poisson distribution.
a) What is the probability of exactly one cough occurring
during this period?
P(X = x) = lambda^x e^(-lambda)/x!
= 2.5^x e^-2.5 /x!
P(X = 1) = 2.5 e^-2.5 = .2052 or 20.52%
b) What is the probability of at least one cough
during a one minute period?
P(X >= 1) = 1 - P(X = 0) = 1 - e^-2.5
= .9179 or 91.79%
c) Based on "theoretical" considerations, do you
think the Poisson distribution is a good model for X? Explain.
We assume that the rate of occurence is constant over
time -- whether or not this is true, it is what the "well known theory"
states (OK, I made this theory up. But it sounds about right to me.)
We assume that the events are indpt of each other. This is tricky.
Probably one person coughing has nothing to do with someone else coughing,
but perhaps one person's cough might affect whether or not that person
coughs again. Still, this assumption sounds like it could be plausible.
(We can always check our data to see if it fits a poisson model. If not,
this might be one reason.) Third, we assume that events can't occur
simultaneously. We can make this a reasonably sound assumption if
we say that we are concerned about the instant a cough begins. It
is unlikely that two coughs begin at exactly the same instance.
d) Here are some data from a study that randomly sampled one-minute intervals in a random selection of flu-season concerts. Use this data to estimate lambda.
1
2
1
2
0
1
2
1
5
2
3
5
3
2
0
Lambda represents the rate of occurence, i.e. the # of coughs per minute. These data are the observed number of coughs in different one-minute intervals. And so a good candidate for an estimate would be to take the average of this. The average of these 15 observations is 2.0.
e) Assume that the Poisson model is a good model for this data. But the exact value of the parameter lambda is in doubt. Do the data above support the hypothesis that lambda=2.5? Write a five-step simulation to provide evidence for or against. Explain how you would make a decision.
1. Box model: The box consists of infinitely
many tickets with the values 0,1,2,.... each in the frequencies determined
by the poisson distribution with lambda = 2.5. Such a "box" exists only
in a computer, and DataDesk, for example, has a random number generator
that generates numbers from this population.
2. Trial: A trial consists of drawing
15 tickets, with replacement, from this box. On DataDesk, this means
choose a random sample of 15 observations from the Poisson(2.5) distribution.
(Under Manip>generate random sample menu.) We then compute the average
3. Def. of a successful trial. In
our study up above, we got an average of 2.0. This is not equal
to 2.5. The question is, do real poisson distributions sometimes
produces averages this far away from 2.5? What's the probability
of this happening? To figure this out, we'll define a successful trial
as one in which the average of a trial is <= 2.0 OR >- 3.0 (which
is the same distance above 2.5 as 2.0 is below it.) In other words, we
are estimating the probability that the observed average is more than .5
coughs/minute away from 2.5, either above or below.
4. Repeat 100 times.
5. The estimated probability is the
number of successful trials divided by 100.
Make a decision: The "null hypothesis"
says that the mean of the poisson is 2.5 and that what we observed, an
average of 2.0, is a common occurence (or at least not unusual.)
If this is true, then the estimated probability should be large-ish to
reflect the fact that this event happens fairly often. So if the
estimated probability is "big" we believe in the null hypothesis. But if
it is small, then we have evidence that this sort of thing doesn't happen
very often, and we should reject the hypothesis that lambda=2.5.
"Big" and "small" are subjective terms, but classically we reject the null
hypothesis if this probability is 0.05 or less.
I did this simulation on my computer. There were 20 cases that were above 3.0 or less than 2.0. So the estimated probability is 20%. This means that this is a fairly common occurence when the mean is 2.5, and so there is no reason to think that the 2.0 we observed is unusual. (In fact, I generated these data from a distribution that was really Poisson with lambda = 2.5.)
6. A bottle-filling machine at the Fizzy Soda bottling and distribution plant is designed to put in 12 ounces of soda into each bottle. In fact, the label on the bottle "guarantees" that it contains 12 ounces of beverage. Because of slight variations, however, the amount it puts in is actually a normal random variable with mean 12.2 ounces and SD 0.2 ounce.
a) What is the probability that a given bottle will
have less than 12 ounces?
Let X represent the amount in a bottle.
Then X is N(12.2, .2) P(X < 12) = P(Z < (12-12.2)/.2) = P(Z
< -1) = .1587 from Table F.
b) Suppose we take a random sample of 6 bottles.
What is the probability that the average amount is less than 12 ounces?
Show all steps.
Let Y be the average of the amount
in the 6 bottles. So Y = (1/6) (X1 + ... + X6) where Xi is the amount in
bottle i. Then
Y is N(12.2, .2/sqrt(6)) or N(12.2,
0.08164965809277261)
So P(Y < 12) = P(Z < (12 - 12.2)/0.08164965809277261)
= P(Z < -2.449) approx. = P(Z < -2.45) = .0071