Name:

SID:

Write clearly and show all necessary work. All questions are worth 5 points, unless otherwise marked.

1. An article in the LA Times in 1997 reports that: "A new study in the May 1 New England Journal of Medicine provides some of the strongest evidence yet that regular exercise helps protect women from breast cancer. The research, conducted in Norway, found that women who exercise at least four hours a week have a breast cancer risk about one-third lower than usual."

a. Is this most likely a controlled experiment or an observational study? Whichever your choice, be sure to explain why this study has the characteristics that make it a controlled experiment or an observational study.

This is most likely an observational study, because the chief characteristic of an observational study is that the patients or subjects sort themselves into treatment groups.  Here the treatment group si the group that exercises 4 or more hours per week, and the "control" group is the group who exercises less.  It's unlikely this exercise regimen could be enforced for long periods of time, so most likely the researchers just observed the exercise habits of the subjects.
 

b. A woman in Norway reads this and decides to exercise at least four hours a week to lower her breast cancer risk. Is it valid to conclude from this study that women who exercise four hours a week will see their breast cancer risk decrease?

This was an observational study, so we can not eliminate the possiblitity that confounding factors might have caused the difference in the two groups.  For example, women who exercise frequently might also take particular care with their diet.  And this diet might protect them from cancer.  (Put slightly differently, women concerned with their diet might also exercise frequently.)
 
 

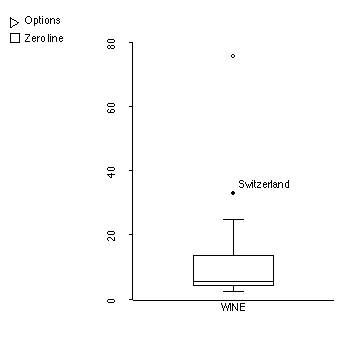
2. So many times, it seems that scientists tell us that something we enjoy is bad for us. That's why the story involving wine and mortality is so refreshing. Finally, perhaps one of our vices will actually be good for us! Below is a boxplot of the number of liters or wine consumed per person per year for 18 "developed" countries. Full details can be found in

A. S. St. Leger, A. L. Cochrane, and F. Moore, "Factors associated with cardiac mortality in developed countries with particular reference to the consumption of wine," Lancet (June 16, 1979): 1017-20.

In case you are thinking of moving, the outlier up around 80 is actually two outliers. France and Italy tied for first place at 79.9 liters per person per year.

a) Warm Up Question: 79.9 liters per person per year: How many liters per day is that? (365 days/year.)

79.9/365 = .219 liters per day

b) Approximately what is the median wine consumption?
The true median is 5.9, but you would only know this from looking at the data.  From the box plot, anything in the range of 5 to 8 would be okay.

c) Is the average wine consumption greater than, less than, or about the same as the median wine consumption for these countries? Explain.

The presence of the outliers pulls the average up, so the average would be greater than the median.  Also, even were the outliers removed, the right-skewed shape of the distribution would mean that the average would be higher than the median. In fact, the average is 16.4.
 

d) Sketch what the histogram for wine consumption could look like.

This is hard to do on the web.  Basically, we were looking for a histogram that had about 50% of it's area between 0 and 7 or so, and then tapered off quickly, with a small bump out near 80.

e) If we removed France and Italy from the data set, how would the average be affected? Will it change more or less or about the same amount as the median?

This has a big change on the average, and makes it quite a bit smaller.  The median is affected only slightly and drops just a little bit.
(The average changes from about 16 to about 9.  The median changes from 5.9 to about 5.5.)
 
 

3. Same data set. Below is a scatterplot of heart mortality and wine consumption.

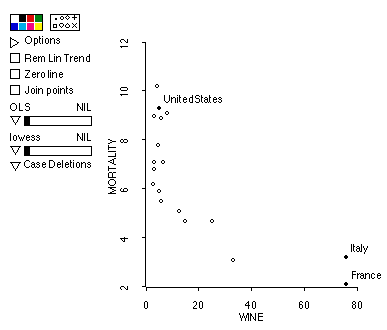
a) Does this graph suggest a relationship between heart mortality and wine consumption? Describe it in words.

Yes.  The relation looks exponential.  Very steep decline in mortality for low levels of wine consumption, and then the slope gradually decreases.
 
 

b) The correlation between heart mortality and wine consumption is -0.7456. Interpret this.

This one was a little tricky.  The correlation is NOT a good measurement of linearity.  What I mean by this is that you can't use the correlation to decide whether or not a relationship is a linear one.  There are some non-linear relationships that produce scatterplots with higher correlations than other linear relationships do.  But, assuming the relationship IS linear, the correlation roughly speaking measures the tendency of the points on the scatterplot to stick close to a straight line.  Another way of thinking about it is that the correlation is measuring the extent of a linear component in the data.  (You can think of a quadratic: y = a + bx + bx^2 as a linear component y = a + bx plus a quadratic component.  If the linear component is "strong", you might get a high correlation.)

The best answer here is that the negative sign picks up on the fact that most countries with above average wine consumption tend to have below average mortality, hence a negative association.  But the value of the correlation doesn't really help us much, since the relation is non-linear.
 
 
 

Shown below is a graph with the Log of mortality and the Log of wine consumption plotted instead of their actual values. (The computer just took the log of each observation.) (The computer mislabels the axes. Should say "Log of Mortality" and "Log of Wine".)

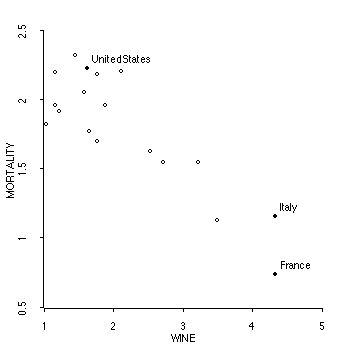And here are the summary statistics for the log of these values:

Data set = Wines, Summary Statistics

Variable N Average Std. Dev Minimum Median Maximum

log[Wine] 18 2.1716 1.0476 1.0296 1.775 4.3294

log[Mortality] 18 1.7833 0.43351 0.74194 1.8707 2.3224

Data set = Wines, Sample Correlations

log[Wine] 1.0000 -0.8593

log[Mortailty] -0.8593 1.0000

Questions appear on the next page.
 
 
 
 

d) Find the regression line for log(Mortality) and log(Wine)

b = r(sy/sx) = (-.8593)*(1.7833/2.1716) = -0.3556
a = ybar - b xbar = 1.7833 - (- 0.3556)*(2.1716) = 2.5555

yhat = 2.55 -0.3556 x

Note that the correlation is much stronger now that we've transformed the data to make it more linear.

e) Interpret the regression line.
 

Be careful here!  Each point represents a country! So your interpretation should reflect this.  The slope means that countries with higher wine consumption tend to have lower heart-related mortality rates.  A country whose log(wine consumption) is one unit higher than another country's will, on average, have a log(mortality) lower by .3556 units.  You can NOT say that increasing wine consumption tends to be associated with decreased mortality, because the data did not measure individuals that increased consumption.  (Similarly, when you have weight on the y axis and height on the x axis, it doesn't make sense to talk about "increasing your height.")
 

f) The United States has a high heart mortality rate. The Wine Is Nutritional Organization (WINO) is launching an advertising campaign designed to increase wine consumption across the US. By how much would heart-related mortality be lowered if we increased our per-capita consumption by log(10 liters per person per year)? Explain.

Almost (but not quite) everyone fell for this.  There is no evidence  that if the US changes it's wine consumption it will have an effect on heart mortality. This was an observational study (it couldn't be anything else), and so the relation could be explained by a variety of confounding factors.  This question cannot be answered from the data presented.
 
 

1, -2, 4 on them. The fourth ball is blue and has the number -2 on it. A ball is selected at random. You win the amount on the ball. (So if -2 is selected, you lose 2 dollars.) Let A be the event that you get a positive number. Let B be the event that the ball is red.

a) Are A and B independent? Show it.
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 

b) Let X represent the amount you win. Write the pdf for X. (You should put it in a table.)
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 

c) What's the expected value of X?