- (a)
- Confidence Intervals
In 1982, the mean crime rate of the 50 states and the District of Columbia
was 5252.71 crimes per 100,000 residents, with a standard deviation of
1500.93. The appropriate confidence interval here is based on a
t-statistic with 50 degrees of freedom, since the variance was estimated
from the data. A 95% confidence interval for the mean crime rate is
(4830.1, 5674.8). Calculations are shown below.
In 1984, the mean crime rate was 4679.67 with a SD of 1330.8. A 95%
confidence interval is (4305.4, 5054.0). It appears that crime rate has
decreased, although since the two intervals overlap, perhaps we can't rule
out the fact that the rate is unchanged.
To check, let's look at a confidence interval for the mean change. Because each state provides two observations (1982 and 1984), we should treat these as paired data. The commands to do this are below. The result is the interval (-675.2, -470.8). Because this includes only negative numbers, we can be 95% confident that the total crime rate has decreased.
xlisp commands to calculate 95% confidence interval for 1982 crime means
(def me (* (t-quant .975 50) (/(standard-deviation totcri82) (sqrt 51)))) ME > me 422.143356328536 > (+ (mean totcri82) me) 5674.84923868148 > (- (mean totcri82) me) 4830.5625260244
xlisp commands to calculate 95% CI for change in crime
> (def change (- totcri84 totcri82)) CHANGE > (def me (* (t-quant .975 50) (/ (standard-deviation change) (sqrt 51)))) ME > (- (mean change) me) -675.242607584417 > (+ (mean change) me) -470.835823788132
- (b)
- Hypothesis Test
The null hypothesis is that the crime rate has not changed, and the alternative is that it has.
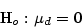
The appropriate test statistic is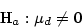
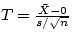 , and our decision rule is to reject the null hypothesis if T is
greater than
, and our decision rule is to reject the null hypothesis if T is
greater than 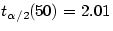 or T is less than -2.01. (I
chose
or T is less than -2.01. (I
chose 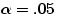 .) The value of the test statistic for these
data is -11.26, and so we clearly reject the null hypothesis.
.) The value of the test statistic for these
data is -11.26, and so we clearly reject the null hypothesis.
Note that there is something funny with this analysis. The data are not a random sample, but instead represent the entire population. Our interpretation of a confidence interval is that if we repeat the experiment infinitely many times, 95% of the time our confidence intervals will cover the true mean crime rate (or true mean change). But what is the experiment here? Where does the randomness come from? One explanation is that the randomness comes from error in the data collection process. In other words, if the FBI were to go out again and collect its data on crime rates, it would do so with some error and so it would differ slightly each time. Note that to collect the data again would require that the FBI travel back in time which, X-files not withstanding, the FBI currently considers to be impossible.
xlisp commands to calculate test statistic
> (/ (mean change) (/ (standard-deviation change) (sqrt 51))) -11.2616921697049
Some of the difficulty with these data is dealing with the missing values and selecting out the men's from the women's scores. To do this, you should have followed the instructions in glossary.html. The actual commands are given below, but the basic idea is to first remove the missing values from satverbal and satmath and gender, and to make sure that you remove the same values from each (so that they have the same length and the ith element of each of these variables comes from the same student. This is not too hard here since the satmath and satverb variables are missing the same entries.)
The two groups do not contain the same people and it seems reasonable to treat these two groups as independent. We'll need to make use of the pooled standard deviation: 13.64
- (a)
- Confidence Intervals
Now, the 95% confidence interval is based on a t-distribution with
45+22-2 = 65 degrees of freedom. (So is the hypothesis test.) The
97.5 percentile for such a t-distribution
is 1.997. (Notice that as the degrees of freedom go up, the 97.5
percentile is
going down. In fact, it is approaching 1.96.) Hence, the CI is (-5.1,
9.1). Because this interval contains 0, there is no evidence of a
difference, even though the men had a
higher average (114.6) than the women (112.6).
xlispstat for defining SAT scores
> (def satverb (select student.dat 2)) SATVERB > (def satmath (select student.dat 3)) SATMATH > (def gender (select student.dat 0)) GENDER > (def satverb (select satverb (which (/= -9 satverb)))) SATVERB > (def satmath (select satmath (which (/= -9 satmath)))) SATMATH > (def gender (select gender (which (/= -9 satverb)))) GENDER > (def sattoal (+ satmath satverb)) SATTOAL > (length sattotal) 67 > (def satfemale (select sattotal (which (= 1 gender)))) SATFEMALE > (def satmale (select sattotal (which (= 0 gender)))) SATMALE > (length satfemale) 22 > (length satmale) 45
xlispstat for calculating confidence interval> (def spooled (sqrt (/ (+ (* (- (length satmale) 1) (^ (standard-deviation satmale) 2) (* (- (length satfemale) 1) (^ (standard-deviation satfemale) 2))) (+ (length satmale) > spooled 13.6428600428074 > (def me (* spooled (* 1.997 (sqrt (+ (/ 1 45) (/ 1 22)))))) ME > (def estdif (- (mean satmale) (mean satfemale))) ESTDIF > (- estdif me) -5.10079809365304 > (+ estdif me) 9.0745354673903
- (b)
- Hypothesis Test
The Null hypothesis is that both groups are the same:
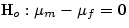 , versus
, versus 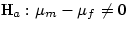 . The appropriate test statistic is
. The appropriate test statistic is
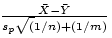 , which we
compare to the 97.5% quantile of a t distribution with n+m-2
degrees of freedom. Here, this means rejecting if the absolute value
of the test statistic is larger than 1.997. The value of the test
statistic for these data is .5598. Hence, we cannot reject the null
hypothesis: there is no evidence of a difference.
, which we
compare to the 97.5% quantile of a t distribution with n+m-2
degrees of freedom. Here, this means rejecting if the absolute value
of the test statistic is larger than 1.997. The value of the test
statistic for these data is .5598. Hence, we cannot reject the null
hypothesis: there is no evidence of a difference.
Again, these data are hardly a random sample. Perhaps it is a random sample from the population of econ majors at this particular college, but even then we don't know how well this result generalizes.