


Next: About this document
Practice for Final
This practice test does not in anyway indicate the breadth or scope
of the exam. It merely provides examples of the types of questions
you might see. It is neither exhaustive nor complete.
- The percentage of hydrocarbons in a sample of beeswax is believed
to follow a normal distribution. Suppose a random sample of
five waxes produces the following list: (each number is the percent
of hydrocarbons in the sample),
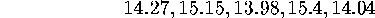
- Assuming that the standard deviation is 0.68 percent, find
a 90% confidence interval for the mean amount of wax.
- Suppose the standard deviation is unknown. Calculate a
90% confidence interval.
- Just to remind you: you should also be able to calculate
the median, quartiles, inter-quartile range of this list.
- Steve the Psychic Pig claims to be able to guess the suit
of a card that you've chosen from a well-shuffled, standard deck
of playing cards, with the jokers removed. (There are 13 of each
suit: hearts, diamonds, clubs, spades.) He grunts once for hearts,
twice for diamonds, thrice for clubs, and four times for spades.
You decide to put him to the test. You will select 10 cards
at random, and he will try to guess what they are without looking.
Let X represent the number of correct answers he gives.
- What kind of variable is X and why?
- What's the probability that he gets 9 or more responses correct?
- What's the probability that he gets less than 30% correct?
- How large does n, the number of guesses, have to be before you
can use the normal approximation?
- Let p represent the probability that Steve gets a card right.
Write the null hypothesis for a test of Steve's psychic abilities.
- Write the alternative hypothesis. Did you choose a one
sided or two-sided, and why?
- We'll use X as our test statistic. Suppose you plan to
reject the null hypothesis if
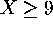 . What's the probability
that you'll mistakenly reject the null hypothesis even though
its true? That is, you'll say Steve is psychic even though he's
just guessing?
. What's the probability
that you'll mistakenly reject the null hypothesis even though
its true? That is, you'll say Steve is psychic even though he's
just guessing?
- Let x represent a student's score on the first midterm, and
y the score on the second. We'll use the 149 pairs of scores
recorded this quarter to fit a regression line that uses the
first score to predict the second. (We're not using
real data here, but the point is the same.)
- If students who do better than average on the first midterm
also do better than average on the second midterm, would the slope
of the regression line be positive or negative?
- What does the intercept of this regression line represent for
this data?
- Suppose the regression line turns out to be

and suppose 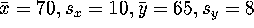 .
What's a? What's the correlation r?
.
What's a? What's the correlation r?
- The students who scored 2 points higher than average on the first
midterm scored, on average, how much higher than average on the second
midterm?
- Define the following:
- mean
- probability distribution function
- parameter
- statistic
- bias
- Give an example of a discrete random variable. Include the
probability distribution function. Compute the mean of this rv.
- Give an example of a binomial random variable. You will be
given brownie points if no one else thinks of the same example.
Explain why this is a binomial random variable.



Next: About this document
Robert Gould
Tue Dec 10 12:55:30 PST 1996
![]()
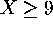 . What's the probability
that you'll mistakenly reject the null hypothesis even though
its true? That is, you'll say Steve is psychic even though he's
just guessing?
. What's the probability
that you'll mistakenly reject the null hypothesis even though
its true? That is, you'll say Steve is psychic even though he's
just guessing?

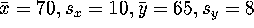 .
What's a? What's the correlation r?
.
What's a? What's the correlation r?