1. This question tests your ability to calculate the correct confidence interval, and also should remind you of the differences between samples and lists.
   1. Since the standard deviation is known (.68 percent), we can use the z interval:

      

      For this particular sample, we find that 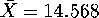, n=5, and from the last row of Table C, 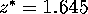. Put it all together, and our confidence interval is (14.068, 15.068).\

   2. Now the standard deviation is unknown, so we have to calculate it using:

      

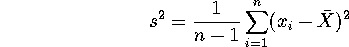
      which turns out to be s = .660 (remember to take the square root to get s from 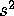). The confidence interval is

      

      where 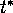comes from Table C, in the row corresponding to 4 df (n-1=4) and the column corresponding to 90%. Thus, 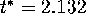. The confidence interval is thus (13.939,15.177).

      The correct interpretation of these intervals is: if you know that the standard deviation is .68, then 90% of all confidence intervals calculated as in part a will contain the true value of the mean. So the interval we found is either one of these that contains the true value, or it is not. There is a 10% chance it is not. If we don't know the standard deviation and have to estimate it, then the same interpretation applies to the wider interval in part b.

   3. The first quartile is 14.04, the third is 15.15, the IQR is 1.11 and the median is 14.27.

2. This question is about hypothesis testing.
   1. You should recognize that X is a binomial random variable; it counts successes in a fixed number of trials, the probability of success is unchanged from trial to trial, and each trial is independent of the last. (We have to assume, and it should have been stated in the problem, that the cards are returned to the deck and the deck is reshuffled each time.) Note that n=10 and, assuming the pig is not psychic but merely guessing, p = .25.
   2. 

      

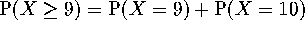
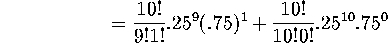
      And this equals 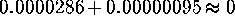. So it's pretty unlikely a pig could get nine or more correct if he's just guessing. So if you saw a pig do this, you'd either have to believe you'd just witnessed a very rare event, or something fishy was going on.

   3. Note that the last problem asked you about counts, i.e. ``how many correct''. This questions asks about proportions: ``what percentage correct." We know that if the pig guesses infinitely many times, he'll get 25% correct. But here he only gets 10 guesses, so we'll let 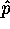represent the proportion correct in this sample. The question then asks you to find .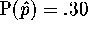

      You can't use the normal approximation here (why not?), so instead notice that if you have 10 trials and 30 percent of them are successess, then you must have had 3 successess. So this question is exactly the same as asking for 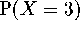. In other words, we've turned it back into a question about counts. The solution is

      

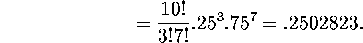
   4. To use the normal approximation, we must have both np and n(1-p) greater than or equal to 10. Since p is smaller than 1-p in this case (p = .25), this will be satisfied if 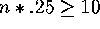, or, in other words, if .
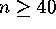   5. The skeptical hypothesis is that the pig is guessing:

      

   6. The alternative hypothesis is that he's not:

      

      This is a one-sided because we're interested in discovering if the pig gets more than 25% of his answers correct.

   7. We're asked to find the probability that you reject the null hypothesis even though its true. Well, if the null hypothesis is true, then p=.25. When do we reject the null hypothesis? The problem tells us we do this if the number of successes is 9 or more, in other words, if 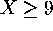. So we want to find 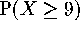when p = .25. But this is exactly the problem we solved in part (b), and so the answer is the same.

3. Some regression questions.
   1. The slope would be positive. You should draw a picture to help you see why this is so.
   2. The intercept in general represents the predicted y value when x=0. Here this means its the average score on the second midterm for students who scored 0 on the first.
   3. You can find the intercept by using the fact that the point 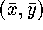lies on the regression line. From this fact we get the formula for the intercept: 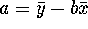which gives a = 98.6. The reason this is so high is because the slope is negative: students who scored well on the first test tended to not score well on the second.

      The correlation is given by remembering the formula for the slope:

      

      so that .

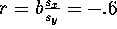   4. The students who scored two points higher than average on the first midterm scored, on average, b*2 = -.48*2 = -.96 points higher, in other words, .96 points LOWER then average on the second. Note that this does not mean ALL of these students scored precisely .96 points lower. It merely means that the average of this group was .96 points below the average for the entire class on the second midterm.

 
• About this document ...