Statistics 10 Lecture 5 Numerical
Summaries II
1. Measuring "Spread"
In addition to knowing the center of a
distribution of data, it is important to know the "spread" or how far
from the center data tends to be.
2. The Standard Deviation (SD)
The Standard Deviation may be thought of as
the average size deviations of the individual values of a list from the overall
average(the mean) of the list. So it's based on the mean.
a. In general, most numbers in a list are
only one standard deviation away from the average. A few numbers will be two
standard deviations away. And very few will deviate beyond that.
STANDARD DEVIATION is abbreviated as SD or as
a lowercase "s".
b. The SD is defined as follows: given a list of n numbers x1, x2, ... , xn,
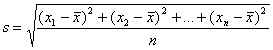or simplified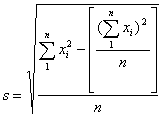 
3. An
Example
An interview with 5 UCLA students reveals the time in hours spent surfing the web in a given week: 7, 17, 3, 14, 7
|
Value |
7 |
17 |
3 |
14 |
7 |
Sum = 48 |
Mean =48/5 = 9.6 |
|
Deviation from Mean |
-2.6 |
+7.4 |
-6.6 |
+4.4 |
-2.6 |
Sum = 0 |
|
|
Squared Deviation from Mean |
6.76 |
54.76 |
43.56 |
19.36 |
6.76 |
Sum=131.2 |
SD= |
= 5.1225
4. More Properties of the Standard Deviation
a . Note that the standard deviation is in the same units
as the data. This is why the standard deviation involves the square root, it allows
for easier interpretation.
b. As with the mean, it is not
necessary to know HOW MANY items are in a list when computing a standard
deviation, only the relative frequency of the values in the list.
c. The SD measures how close the
numbers in the list are to the average; i.e., not all numbers are equal to the
mean; the SD is a measure of the "average" distance between each
point and the overall average.
d. Another thing about the standard
deviation. For many datasets 68% of the entries on a list will fall within one
SD of the average. 95% of the entries will fall within two SD of the average.
But we'll talk about this some more in Chapter 5.