Textbook Example 5

Correlation

What is a Correlation?

Correlation is simply a measure of the strength of a relationship between two variables. Correlation measures the linear relationship between the variables; the degree to which their data points fall onto a straight line. The most common correlation measurement is the Pearson coefficient "r " (there are others).

The Correlation Coefficient

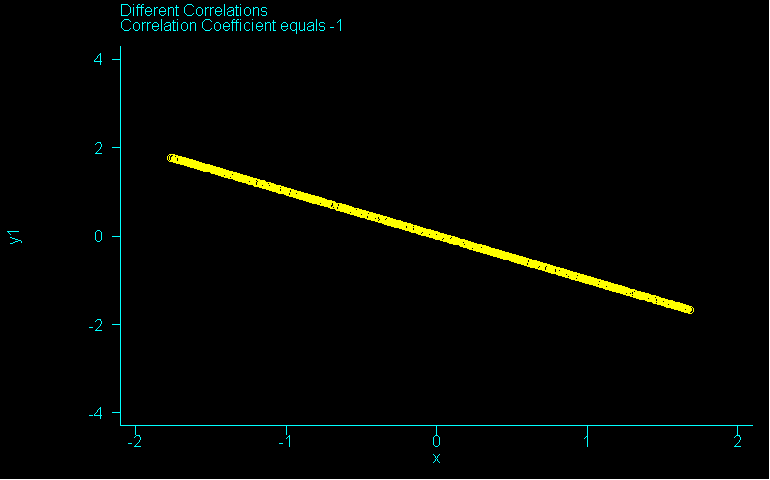
A correlation coefficient "r " reveals two things; the strength of the relationship and the direction of the relationship. If two variables have a perfect correlation (their data points fall onto a straight line), then r =1.0 (positive correlation) or r=-1.0 (negative correlation)

The positive and negative values simply show the direction of the relationship. When two variables are positively related, as one increases, the other also increases. When they are negatively related, as one increases, the other decreases. Two variables with less than a perfect correlation will have an "r value" between 0 and 1.0 or 0 and -1.0. If no relationship exists between two variables, r = 0.

The graph below shows a perfect negative correlation, if you want to see this animated, just click on the picture. It will run through correlations from -1 to 0 and up to 1 and back again. It might take a minute to load.

Question 1. (TRUE OR FALSE) A correlation coefficient tells you what percentage of observations ("points") are on a straight line.

Question 2. (TRUE OR FALSE) A correlation of +.50 is stronger than a correlation of -.80

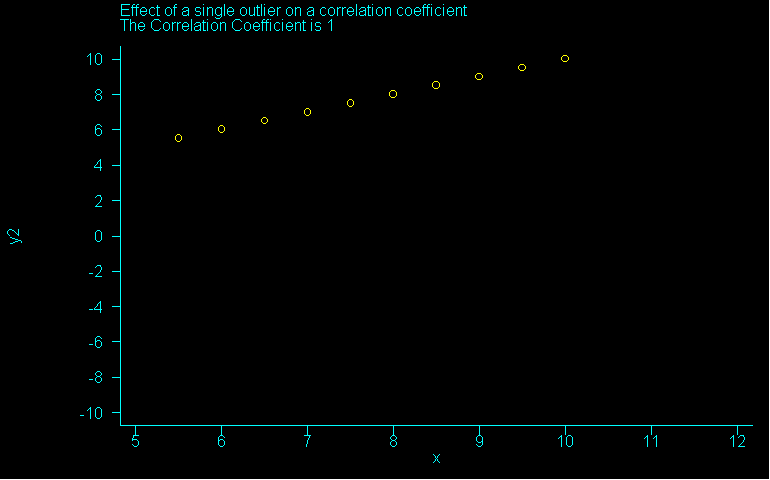
Outliers (or extreme observations) do not "fit" within the general distribution of a variable. They are important observations and should not be ignored because they are often the source of problems by distorting averages, standard deviations etc. The next graphic shows the effect of outliers on the correlation. If you want to see this animated, just click on the picture.

Question 3. (TRUE OR FALSE) A correlation of 0 always means that there is no relationship between variables X and Y.

Question 4. (TRUE OR FALSE) It is possible to dramatically change a correlation by changing a single value.