Textbook Example 1

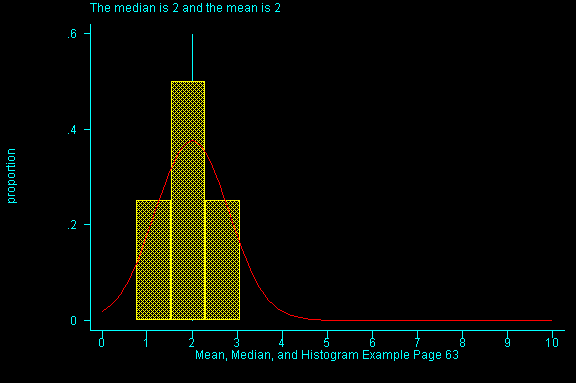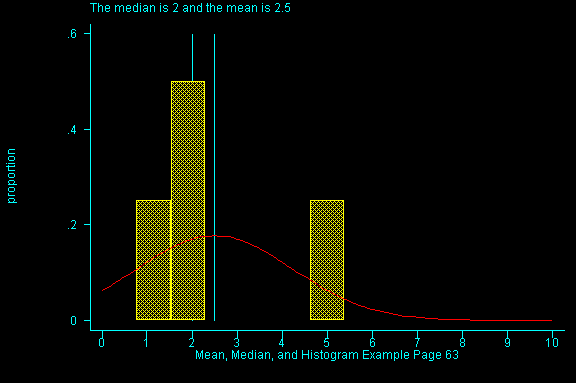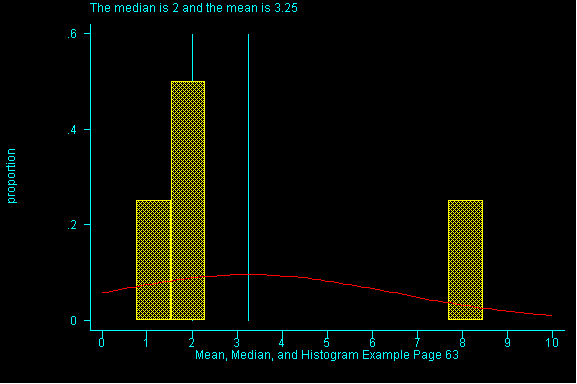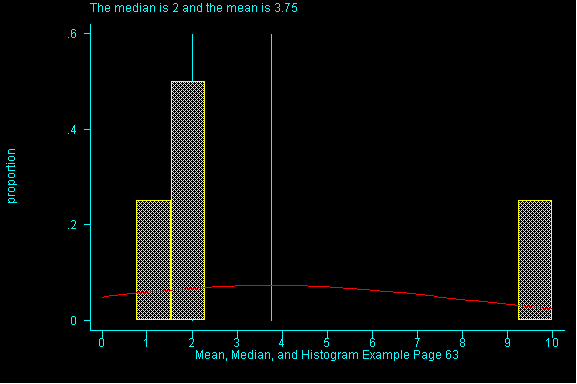
Statistics provides a common language for the "shape" or "pattern" of data. A symmetric dataset is one in which if you were to divide it into two pieces through its center, the resulting pieces would be mirror images.

When the pattern of data is symmetric, the mean (or average) will be equal to the median. When data is skewed the pattern of data is off-center. If it is skewed to the right (i.e right-skewed), higher values are more spread out than lower values in the dataset and the mean will have a larger value than the median. (See Figure 1)

                                                The effect of spreading out the higher values in a dataset, note the
                                                                difference between the mean and the median.

Please answer the following thought/reasoning questions:

Question 1: Suppose the values in a dataset are "left-skewed". In plain English, please describe a graph of left-skewed distribution of data.

Question 2: Suppose the values in a dataset is "left-skewed". What is the relationship of the mean to the median in this case? To see an example, click here

Question 3: Please provide some examples of "right-skewed", "symmetric" and "left-skewed" data that we might encounter in every day life. If this seems difficult, try visiting a web site such as CNN News or YAHOO! News and type the words "average" and "median" (no quotes) in the search window.

Question 4: Consider the lecture on means and medians, if you were an employee trying to maximize your salary, which statistic on worker's salaries (the mean or the median) would you present to make your argument to your employer? Why? Suppose you were the employer which salary statistic (mean or median) would you prefer to present to employees and their salaries if you were trying to keep salaries low?