Textbook Example 2
What does the Law of Averages really say to you?
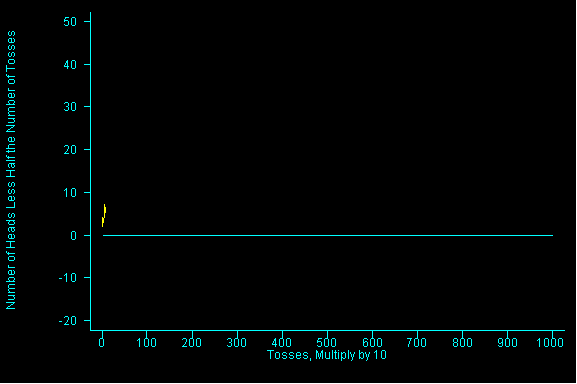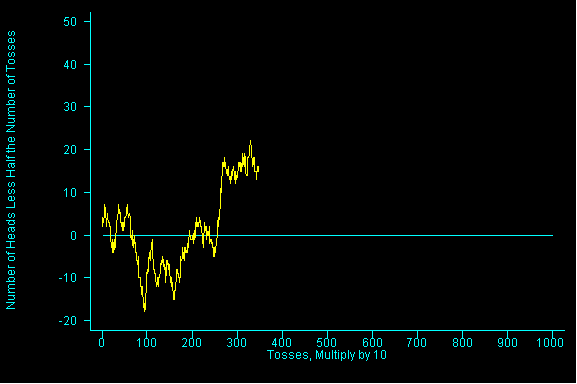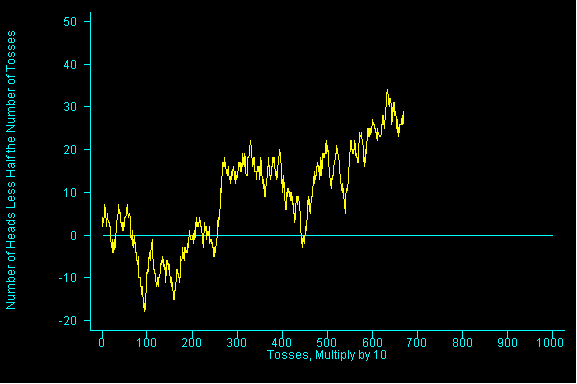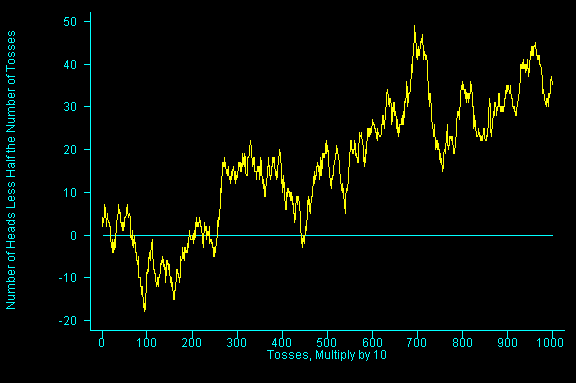
This example is taken from the textbook, recall than Mathematician John Kerrich flipped a coin 10,000 times.We are duplicating that experiment in this example. Here, we are tossing a coin 10,000 times by keeping track of every 10 tosses and counting up the number of heads in the 10 tosses. We repeat this 10 toss procedure 1,000 times.
Here is what is being graphed, the horizontal line at zero represents the place where the number of heads is exactly equal to the number of tails.
Values below the line represent times when the total number of heads was less than the total number of tails.
Values above the line represent times when the total number of heads was greater than the total number of tails.
The idea behind this example was to debunk a misunderstanding about the "law of averages". That is the actual number of heads will not equal the number of tails. This is caused by chance error.
In the next example, the PERCENTAGE or PROPORTION of heads is being graphed against the number of tosses. This illustrates a truth about the law of averages.
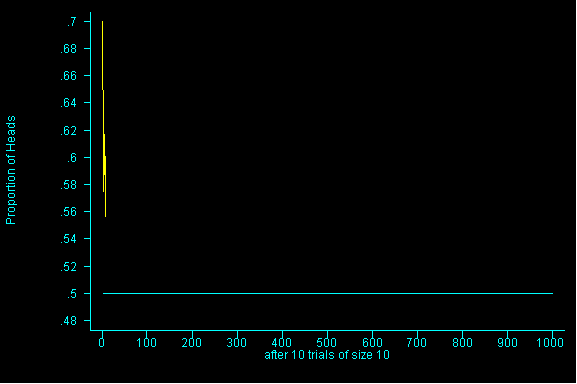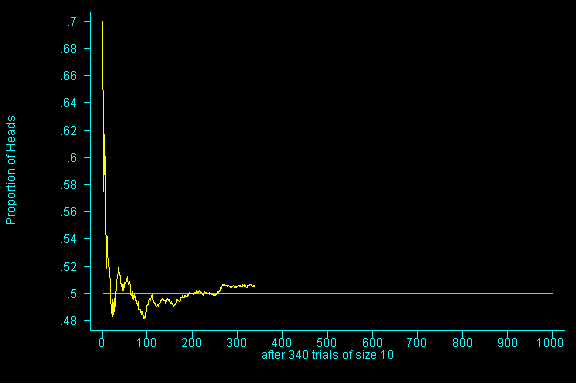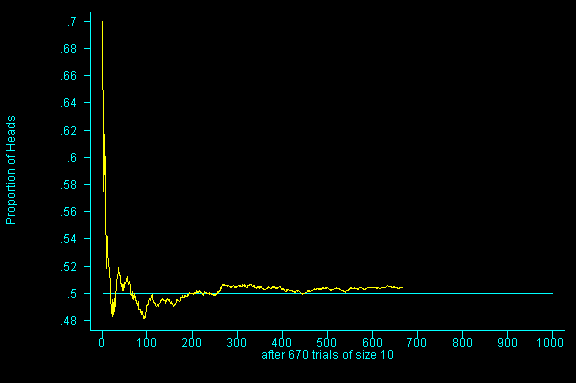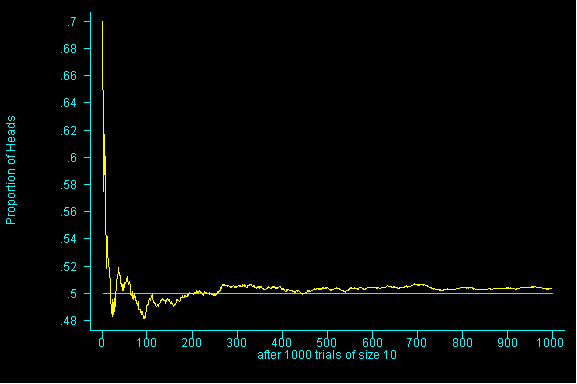
What is true is that the long run PERCENTAGE grows closer and closer to 50 as the number of tosses increases. So while we may be further and further "off" if we are looking at the actual "count" of heads, percentagewise, in the long run, we grow closer and closer to the expected 50%.
This is a very subtle point and perhaps it is easiest to understand if you consider the fact that we "live in the short run" and while we EXPECT the same number of heads and number of tails in a given set of tosses, this may not necessarily occur.
The next table is designed to give you a sense of where misunderstandings about the "law of averages" arise. We have tabled the count of heads in 10 tosses for all 1,000 times we tossed a coin 10 times:
# heads out | of 10 | tossed | Freq. Percent Cum. ------------+----------------------------------- 0 | 1 0.10 0.10 1 | 9 0.90 1.00 2 | 29 2.90 3.90 3 | 128 12.80 16.70 4 | 213 21.30 38.00 5 | 242 24.20 62.20 6 | 190 19.00 81.20 7 | 131 13.10 94.30 8 | 48 4.80 99.10 9 | 8 0.80 99.90 10 | 1 0.10 100.00 ------------+----------------------------------- Total | 1000 100.00Sure enough, 5 out of 10 is the most common outcome, but it is clearly not something that happens 100% of the time, nor does it even happen 50% of the time. In fact, if we graph the outcomes, take a look at the image which arises:
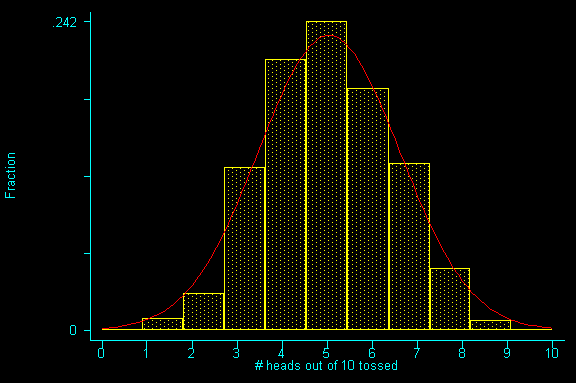
Look familar? We have drawn a normal curve over it so you can compare.
ASSIGNMENT
This part is an exercise in constructing a box model. Before you start this, you should have finished reading Chapter 16, especially 16.4.
This is a review on what you have learned from Freedman
(1) I would like you to sketch a box for the game of "roulette" but using the guidelines in Review Problem #8 (page 286) on placing what is called a "Four Number Bet" in the language of Las Vegas.
Here, you are wagering your money between four numbers. The numbers again must all touch at one point on the layout (see page 282). The payoff for a four-number bet (often called a square bet) is eight to one. In other words, a $1 bet will yield $8 if one of your four numbers win.
From what you have learned about constructing boxes, please construct a box for this kind of bet.
Then answer the following:
(2) Should you be replacing the tickets after each draw? If yes, explain why. If no, explain why not.
(3) Suppose you are going to play roulette 100 times (or bet $100 one dollar at a time). Calculate your net gain after 100 plays. You should probably use review problem #8 to help you with this one.
(4) Once you have #3 then consider this problem: suppose 100 people were to walk into the casino and play roulette exactly the way you did in #3. How much money do we expect all 100 people to have after playing 100 times?
Write these numbers down and turn in the whole assignment.
If you would like to learn more about roulette, please see:
http://www.goingtovegas.com/kpv-roul.htm
Please remember to read Freedman's summary on page 287 of your text.