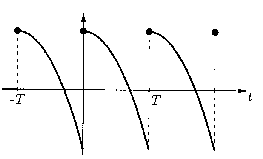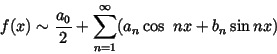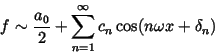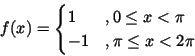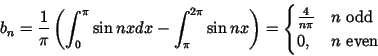Definition 1 (Periodic functions)
A function f(t) is said to have a period T or to be periodic with period T if for all t,
f(t+T)=f(t), where T is a positive constant. The least value of T>0 is called the principal period or the fundamental period
or simply the period of f(t).
Example 1
The function
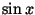
has periods
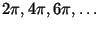
,
since
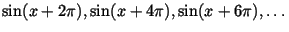
all equal
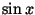
.
Example 2
Let
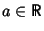
.
If f(x) has the period
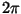
then
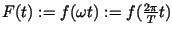
has the period
T.
(substitute
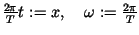
)
Example 3
If
f has the period
T then
Definition 2 (Periodic expansion)
Let a function
f be declared on the interval [0,
T). The
periodic expansion 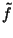
of
f is
defined by the formula
Definition 3 (Piecewise continuous functions)
A function f defined on
I=[
a,
b] is said to be
piecewise continuous on
I if and only if
- (i)
- there is a subdivision
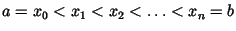 such that f is continuous on each subinterval
such that f is continuous on each subinterval
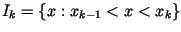 and
and
- (ii)
- at each of the subdivision points
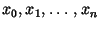 both one-sided limits of
f exist.
both one-sided limits of
f exist.
Theorem 1
Let
f be continuous on
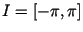
.
Suppose that the series
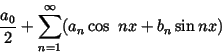 |
(1) |
converges uniformly to
f for all
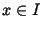
.
Then
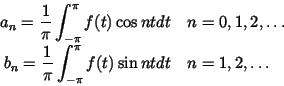 |
(2) |
Definition 4 (Fourier coefficients, Fourier series)
The numbers
an and
bn are called the
Fourier coefficients of
f.
When
an and
bn are given by (
2), the trigonometric series (
1)
is called the
Fourier series of the function
f.
Example 4
Let
f(
x) be defined in the interval [0,
T] and determined outside of this interval
by its periodic extension, i.e. assume that
f(
x) has the period
T. The Fourier series
corresponding to
f(
x) (with
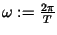
)
is
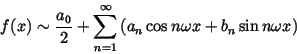 |
(5) |
where the Fourier coefficients
an and
bn are
 |
(6) |
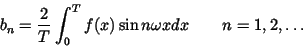 |
(7) |
Example 5
Let
an and
bn be the Fourier coefficients of
f, see above.
The
phase angle form of the Fourier series of
f is
with
amplitudes
and
phase angles
See the
applet to gain intuition as to the effects of the amplitude and the phases on the function behavior.
Example 6
We compute the Fourier series of the function
f given by
Since
f is an odd function, so is
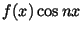
,
and therefore
a0=0
For
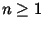
the coefficient
bn is given by
It follows
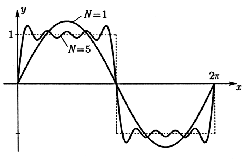
The Gibbs Phenomenon
Developed by Marian Prutscher: Email