Introduction
We present a novel MCMC inference algorithm called Clustering Cooperative and Competitive Constraints (C4) to solve the problem of finding multiple solutions in graphical models. C4 builds upon Swendsen-Wang clustering to cluster strongly coupled sub-solutions in graphical models and swaps them with competing sub-solutions, allowing it to jump between multiple modes in the posterior and thus achieve a fast mixing time. It also retains multiple solutions to avoid premature commitment to a single solution that may not be valid given later context. Locally compatible values for vertices in the graph are probabilistically clustered and swapped simultaneously with other locally compatible groups that conflict with each other. By updating competing clusters simultaneously, C4 can not only jump out of local minima more easily than comparable MCMC methods, but can also find multiple solutions, i.e. significant modes in the Bayesian posterior probability. This is critical for mid-level vision tasks in which there may be ambiguous interpretations at an early stage and we want out algorithm to avoid premature commitment until more context is present. We present the formulation of C4 on general graphical models as well as hierarchical models and show that it outperforms Swendsen-Wang clustering, Gibbs sampling, Iterated Conditional Modes, and Loopy Belief Propagation on MRFs, CRFs, and hierarchical graph models with positive and negative constraints. We also find that C4 outperforms other MCMC methods in finding a minimum energy solution, even for energy functions with only one significant mode, due to its ability to jump out of local minima and move quickly through the solution space.
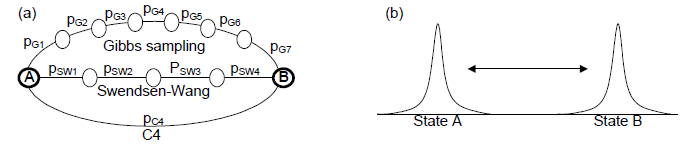
figure 1: the use of both cooperative and competitive constraints allows C4 to make larger moves through the solution space than traditional Swendsen-Wang or single site samplers, and therefore can find modes in the distribution more quickly.
Background
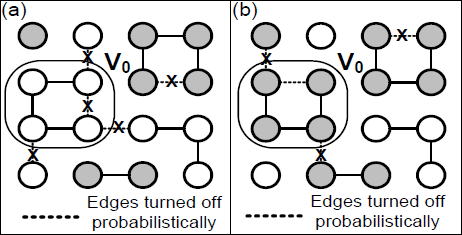
figure 2: an example of the Swendsen-Wang algorithm. (a) Edges turned off probabilistically, indicated by dashes, to form a connected component. (b) Recoloring of a uniformly selected connected component.
The original Swendsen-Wang algorithm was designed to speed up single site Gibbs sampling. In particular, Swendsen-Wang is very efficient for sampling the Ising model, which consists of a lattice of nodes that have two "spin" states and pairwise connected to the four nearest neighbors. The Swendsen-Wang algorithm is derived by introducing an auxiliary variable the Ising probability model that represents edge states of "on" and "off". Sampling is achieved by alternatingly sampling from the two conditional probabilities: node states given edge states, and edge states given node states.
This works out to have a very elegant solution that can be efficiently computed. When sampling the edges, each edge can be sampled independently according to a very simple probability. To sample the nodes a connected component is selected uniformly from the remaining edges and all nodes in that component are relabeled to the opposite spin.
Negative Interactions
In Swendsen-Wang our algorithm converged very quickly by grouping compatible labels together based on their similarity. But what if we have a constraint that requires that two neighboring sites have different labels? How should we incorporate these negative interactions into Swendsen-Wang?
Figure 1 shows an example of a system with negative interactions. We are still looking at a two-label Ising model, but now we have a number of negative edges requiring that neighboring sites have different labels. Assuming that we’ve already gotten into a compatible state, Figure 3 shows why each of the commonly used MCMC algorithms breaks down in trying to sample alternate configurations. In (a) we see that Gibbs sampling attempts to update one site, which creates a low probability state, and thus is not likely to be accepted. Swendsen-Wang improves slightly in (b) by selecting an entire cluster of sites grouped along positive edges, but creates a configuration that would now violate the negative edges, and thus will not likely be accepted. C4, shown in (c), however, can handle this situation by identifying the positively grouped sites and updating the conflicting clusters simultaneously so that the negative constraints are satisfied.
C4 Algorithm
We propose to solve the problem of slow convergence with negative interactions with our algorithm, C4. Figure 3 shows an example of applying C4 to a checkerboard pattern Ising model with both positive and negative interactions. We turn edges on and off probabilistically as in Swendsen-Wang, as shown in (b). Once we select a component, however, we can break it into sub-components of positively associated vertices. These sub-components are all negatively related, implying that they need to be differing values. This is shown in (c). We essentially break a large CSP into a smaller sub-problem using probabilistic clustering and constraint satisfaction.
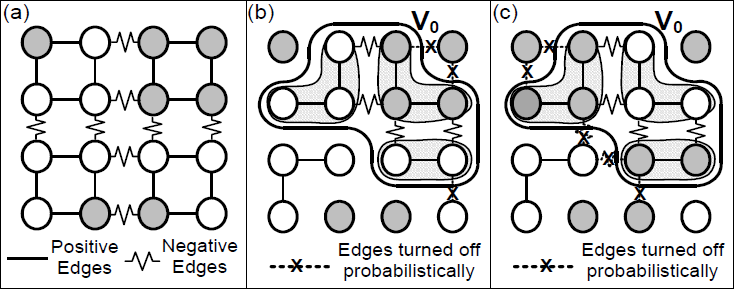
figure 3: Example of C4 on the negative edge Ising model. (a) Initial state of the system. (b) Edges probabilistically turned on and off. (c) The selected connected component V0 and its resulting sub-components, consisting of similarly labeled vertices connected to other sub-components by negative edges
Experiments with C4 on the Ising and Potts Models
In this section we demonstrate C4’s performance on the Ising and Potts models with both positive and negative edges compared to Gibbs sampling, SW sampling, and belief propagation.
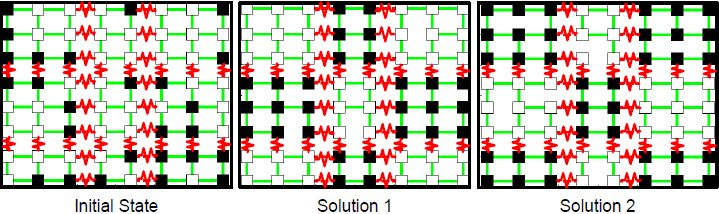
figure 4: checkerboard test pattern with negative constraints. This example has two minimum energy modes, shown in Solution 1 and Solution 2
Figure 4 shows a 2D Ising model with both positive and negative edges. The ideal labeling of the nodes is in an alternating checkerboard pattern, though there are two equally probable solutions that satisfy this constraint. To get a better idea of C4’s performance in finding the two solutions in Figure 4, Figure 5 shows a sampling animation for C4, Gibbs sampling, SW, and BP. We can see that C4 converges the fastest of all four algorithms in a mere 10 iterations or so. Belief propagation cannot converge due to the loopiness of the graph and Gibbs sampling and Swendsen-Wang cannot quickly satisfy the constraints as they do not update enough of the space at each iteration. This shows that C4 has a very low burn-in time (in this case, none is needed), whereas Gibbs sampling needs a couple hundred iterations thrown out before it draws unbiased samples.

figure 5: animation of all four algorithms working on the checkerboard Ising problem from the same initial state.
We ran the same experiment as with the Ising model above but this time solved the same checkerboard pattern on a Potts model in which each site could take one of seven possible colors. When using the Potts model, the relabeling can no longer be a deterministic flip, and instead must undergo a Metropolis-Hastings rejection step for recoloring V0. In this case we use random sampling for relabeling V0.

figure 6: animation of all four algorithms working on the checkerboard Potts problem from the same initial state.
Once again we see that the convergence rates are comparable to the Ising case, with C4 far outperforming the other algorithms. This is shown in Figure 6. Unlike in the case of the Ising model, however, Swendsen-Wang is also able to find multiple solutions this time. This is because the Potts model is less constrained than the Ising model, allowing neighboring sites to have a number of different values, just not the same value. This means that SW can update a block of the checkerboard without necessarily violating constraints. However, when we look at the plot of correlation over time on the right of Figure 10, we see that Swendsen-Wang is still far more highly correlated than C4 is. While C4’s correlation looks like a low, randomly walking line, SW’s correlation gets stuck in peaks, meaning that it either doesn’t move for a couple of iterations, or is not moving very far within the space from step to step. Thus C4 still mixes, not only faster, but more thoroughly.
References
IEEE Trans. on PAMI (accepted), 2010.
Physical Review Letters, 1987
PAMI, 1984
Lecture Notes in CS, 2006