Summer Research Project
Adjusting Active Basis Model by Regularized Logistic Regression

Ruixun ZHANG (zhangruixun@gmail.com)
Dept. of Statistics and Probability
School of Mathematical Sciences
Peking University

Mentor: Prof. Ying Nian Wu
Superviser: Zhangzhang Si

Active basis model is a generative model seeking a common wavelet sparse coding of images from the same object category, where the images share the same set of selected wavelet elements, which are allowed to perturb their locations and orientations to account for shape deformations.

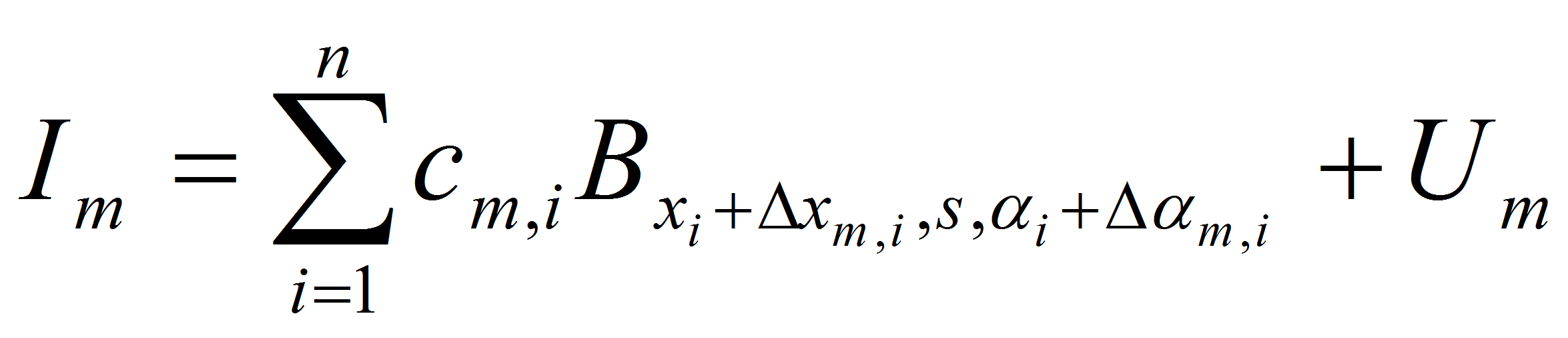
To specify the probability distribution of image intensities, we assume

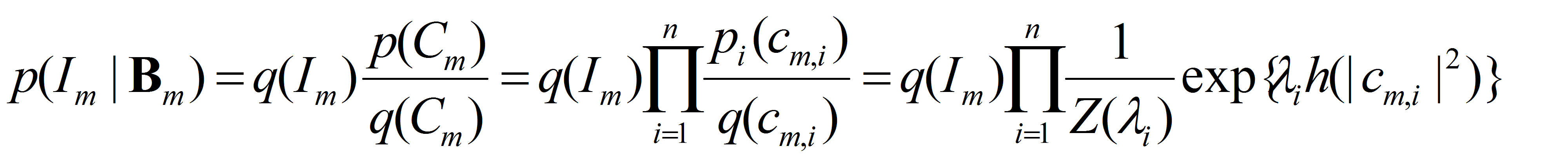
which is the bottom layer of the generative model, where we assume that conditional on B_m, the coefficients are independent under both p(I) and q(I). Treating q(I) as the distribution of negative examples, log p(class = + | I)/p(class = -| I) is linear in the sigmoid h of MAX1 scores (maxing out the perturbations) of the selected basis elements, with lambda's being the coefficients of the logistic regression.

In learning the active basis model, we do not need negative examples from q(I), except pooling a marginal histogram q(c) or q(r) where r = |c|^2. The generative learning in this context is defined by arg-max inhibiting in the shared sketch algorithm. It estimates lambda's by maximum likelihood, so that the learned active basis model can be used for classification and detection. That is, it can stand alone with well-defined and easily computable likelihood for both learning and inference, without the need for negative examples or discriminative learning.

After selecting the basis elements, we can nonetheless bring in the negative examples, and re-estimate the lambda parameters of the active basis model by fitting the logistic regression. The re-estimation helps to correct the aforementioned conditional independence assumption. Since it is done on the basis elements selected in generative learning that hugely reduces the dimensionality, the discriminative adjustment is very efficient.

This work applies discriminative methods to adjust lambda parameters of selected basis elements, including (1) logistic regression, (2) SVM and (3) AdaBoost. Results on supervised learning show that discriminative post-processing on active basis model improves its classification performance in terms of testing AUC (area under ROC curve). Among the three methods the L2-regularized logistic regression is the most natural one and performs the best.

The L2-regularized logistic regression is natural because the logisitic regression follows from the above exponential family model, and the likelihood p(class | image) of the logistic regression can be understood as partial likelihood of the full model p(class, image) = p(class) p(image | class). The L2 regularization leads to Stein's shrinkage and smoothness of lambda's, that is, we want the weights of the selected basis elements to be small and similar to each other (ideally, they should be the same if the strokes are all on the shape boundaries).


Report for my project. pdf docx
Slides for my presentation. pdf pptx
Poster. pdf pptx
Source code is attached in each experiment. Quick downloads for code and data: head/shoulder guitar butterfly motorbike horse
System requirement: at least 4GB of memory is needed (6GB or above recommended).


1. Methods
We use active basis model [1] to learn a template of 80 Gabor elements (B1,¡­,B80), with local normalization of Gabor filter response, and then adjust paramter ¦Ë¡¯s of selected basis elements based on MAX1 scores after sigmoid transformation using discriminative criteria. After dimension reduction by active basis (from about 1 million features down to only 80), the computation is fast for discriminative methods.

1.1 Logistic regression. We use Lin's liblinear logistic regression package [2, 3] with L2 regularization. The model is

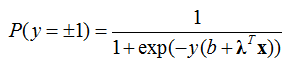
where y is the label of an image (-1 or 1), x are selected (by Active Basis model) MAX1 scores (locally maximized Gabor responses) after sigmoid transformation, ¦Ë is the regression coefficient and b is the intercept term. The loss function is

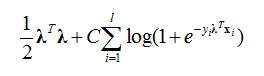
where the intercept term is included in the regularization term.
However, we want L2-regularization (corresponding to a Gaussian prior) without the intercept term, so we modified the codes slightly to make loss function:
.
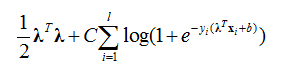In the training process, the images share the same data weight 1.
Also, classification performance is not sensitive to the tuning parameter C when C is small. So C is set to 0.01 in the experiment. (see discussion in section 3)

Modifications in the liblinear code: The original implementation of liblinear enforces regularization on all linear coefficients including the bias term (if the bias term option is enabled). However, in our experiment this is not desirable, because we want to allow a large bias term in the case where positive and negative data is unbalanced. Following Lin's suggestion, we make a small modification on the liblinear package:

For the three functions

replace "i < w_size" with "i < w_size-1" in the FOR loops. This simply neglects the bias term when calculating the L2 regularization penalty.

1.2 SVM. We use SVM [4] from Joachims's SVM-light [5] with bias term and linear kernel. Classification performance is not sensitive at all w.r.t the tuning parameter C, which is then set to 1 in the experiment.

1.3 AdaBoost. We use the AdaBoost [6] implementation in experiment 3 of active basis model.

1.4 Logistic regression vs. other methods. The following figure [10] compares loss functions of the above-mentioned methods.

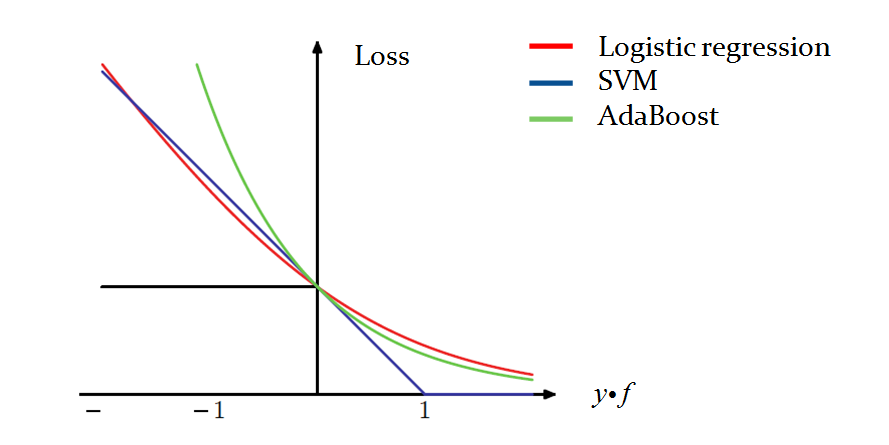
Generally there are 2 common ways to add regularization: L1-regularization and L2-regularization. Friedman [10] points out that L1-regularization is preferred when the goal is to find a sparse representation, but since in our case basis elements have been already selected in generative learning, we want to use L2-regularization for smoothness instead of sparsity.

Furthermore, L2-regularized logistic regression is similar to SVM, and L1-regularized logistic regression is similar to AdaBoost [8, 9, 10, 13]. This is shown in the above figure, where the cost functions of the three methods are similar for 0-1 losses. Logistic regression is readily formulated in likelihood-based learning and inference, where the joint probability of data and label is trained towards good classification performance. While AdaBoost and SVM adopt a smartly designed cost function (exponential loss in the case of AdaBoost, and margin in the case of SVM), instead of the generic probability form. So we say logistic regression is more natural than the other two methods. In our experiment, we find that logistic regression consistently performs the best.

In our future work, we will apply the adjustment procedure to unsupervised learning. We use the generative active basis model in the presence of hidden variables (unknown sub-categories, locations, poses, and scales). Then we re-estimate ¦Ë¡¯s by fixing the inferred hidden variables in learning as well as selected basis elements. As a consequence of generative model, we fit a flat logistic regression. With hidden variables given and basis elements selected, the learning becomes supervised.


2. Classification Experiments
Here is the code for head/shoulder classification experiment.

General learning problems should be unsupervised (examples in experiment 4 and experiment 5), but here we work on supervised learning as a starting point.

2.1 Dataset. For the head_shoulder dataset, we tried 4 methods for classification:

The following figure shows several positive examples in the head_shoulder dataset.


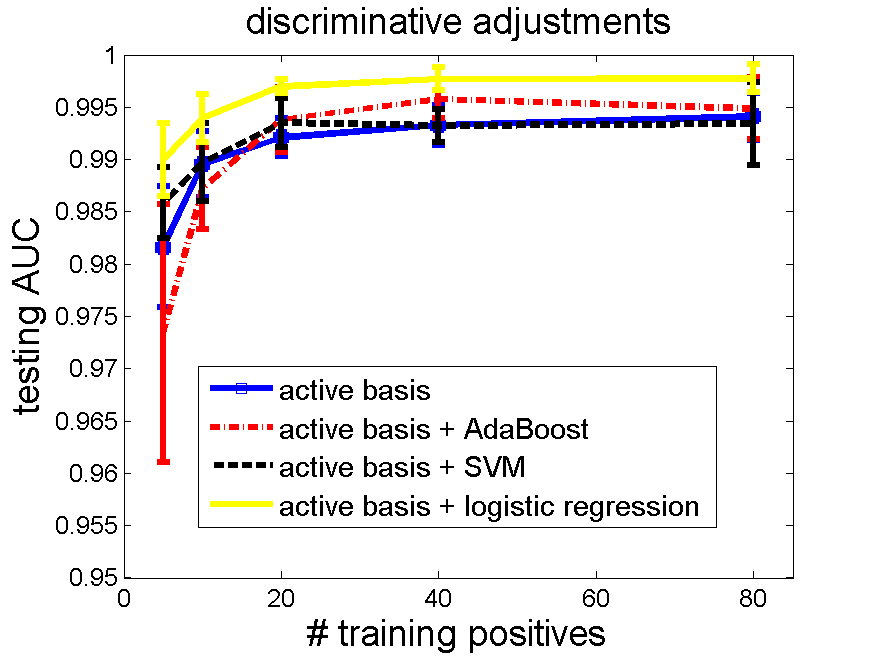
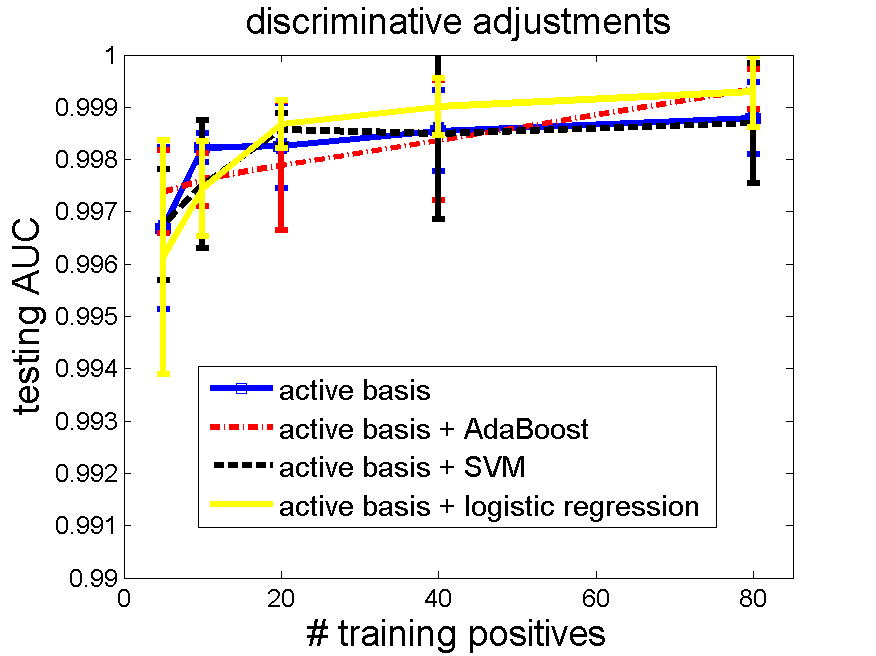
2.2 Results of testing AUC. Number of selected elements 80, training negatives 160, testing negatives 471. In total, 5 repetitions (randomly split the data) * 4 methods * 5 numbers of positive training examples (5, 10, 20, 40, 80) are tested. The testing AUC is plotted below. Logistic regression is the only method that consistently improves active basis model.


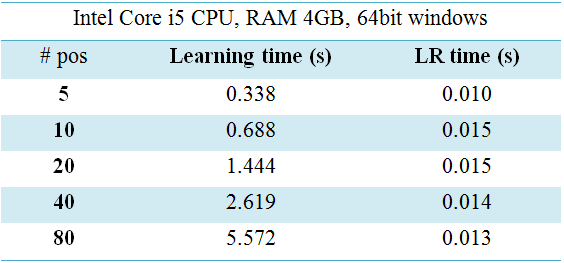
2.3 Computing time. The feature selection step in active basis model has greatly reduced the dimension of an image from millions of features to dozens of basis elements (in this case 80), so the computing time for discriminative adjustments is short. The table below shows the time of one active basis learning, and one logistic adjustment after SUM1 and MAX1 step.



3. Tuning Parameter - Overfitting without Regularization
The un-regularized logistic regression does not work well on the feature selected by active basis model. It worsens instead of improves the classification performance of the active basis model. The following figure shows the testing AUC's.


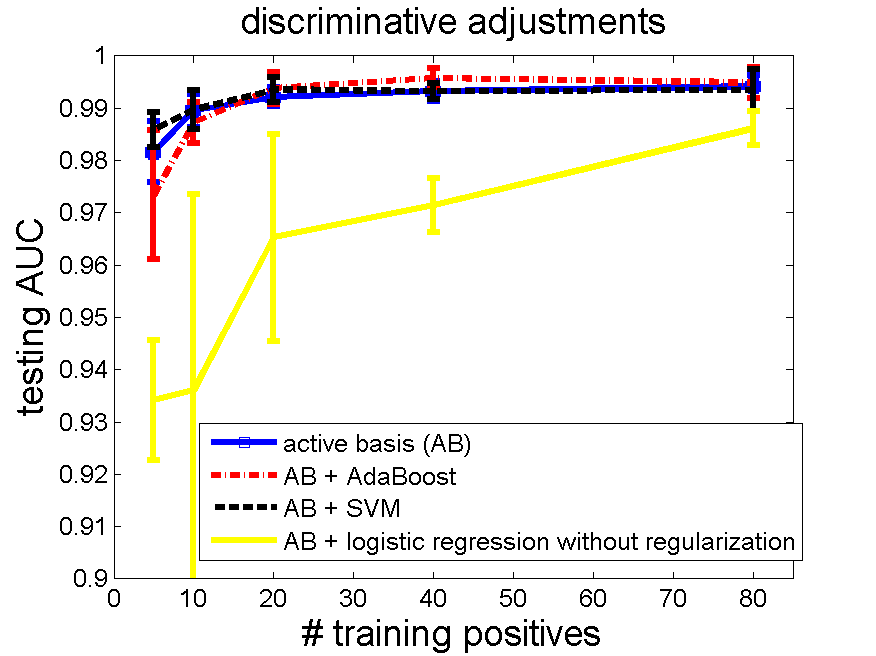
We suspect that logistic regression suffers from overfitting, which is the very motivation of adding a L2-regularization term.
In order to verify this, we test different tuning parameters for L2-regularized logistic regression. See figure below.
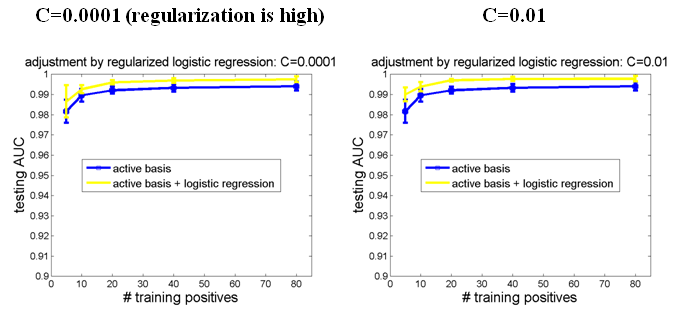
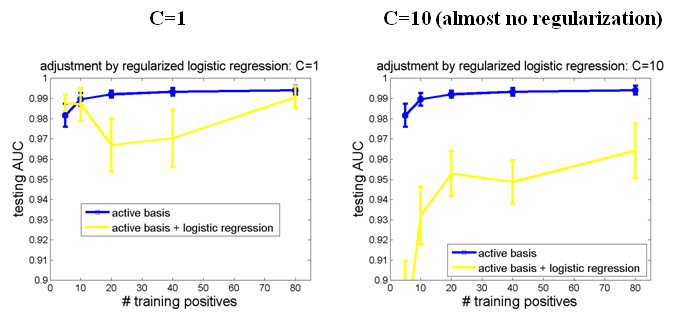
The yellow line is the testing AUC after adjustment by logistic regression. From these figures we can draw the following conclusions:


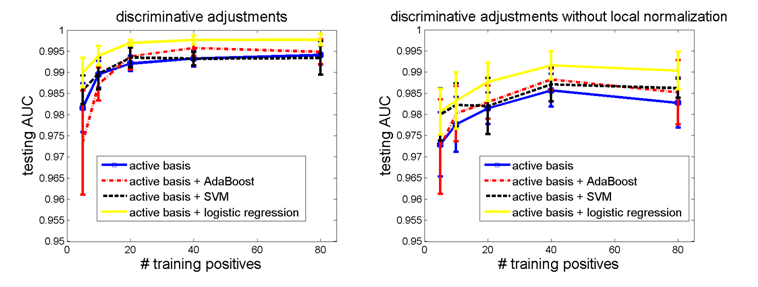
4. With or Without Local Normalization
We also investigate two versions of Gabor feature responses: a simple saturated Gabor response vs. locally normalized Gabor response. The following 2 experiments compare the two versions of features. It is clear that local normalization helps classification.


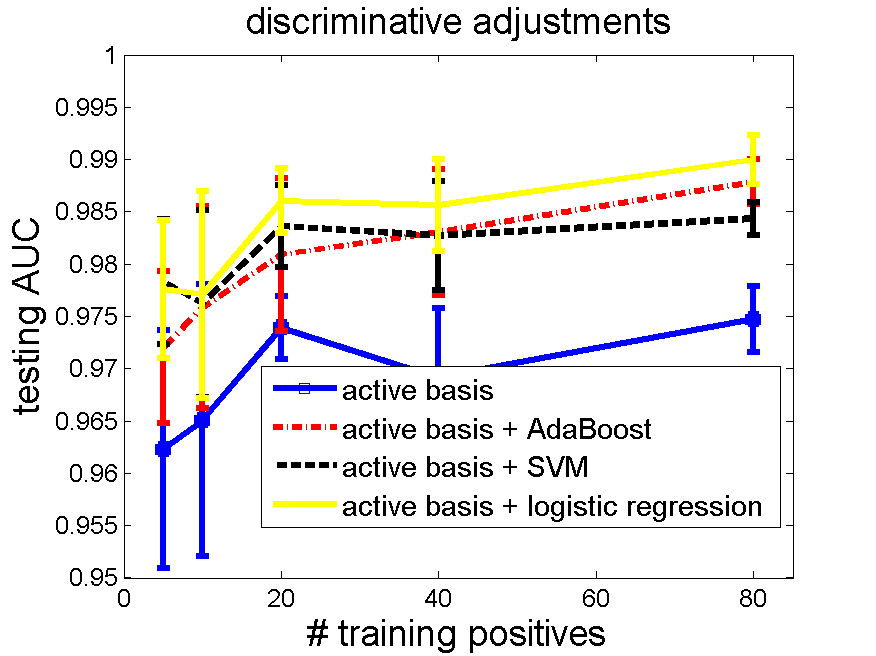
5. Experiments on More Datasets
We repeat the classification experiment for other datasets. The following figures show similar results as in head_shoulder.

5.1 Horse. Number of selected elements 80, training negatives 160, testing negatives 471. code




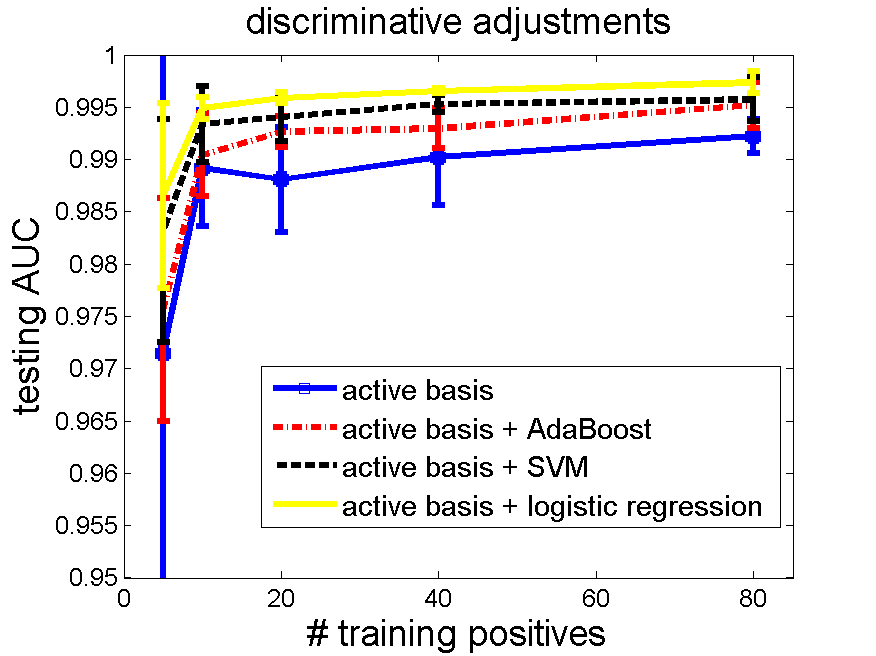
5.2 Guitar. Data is from Caltech 101 [12]. Number of selected elements 80, training negatives 160, testing negatives 855. code




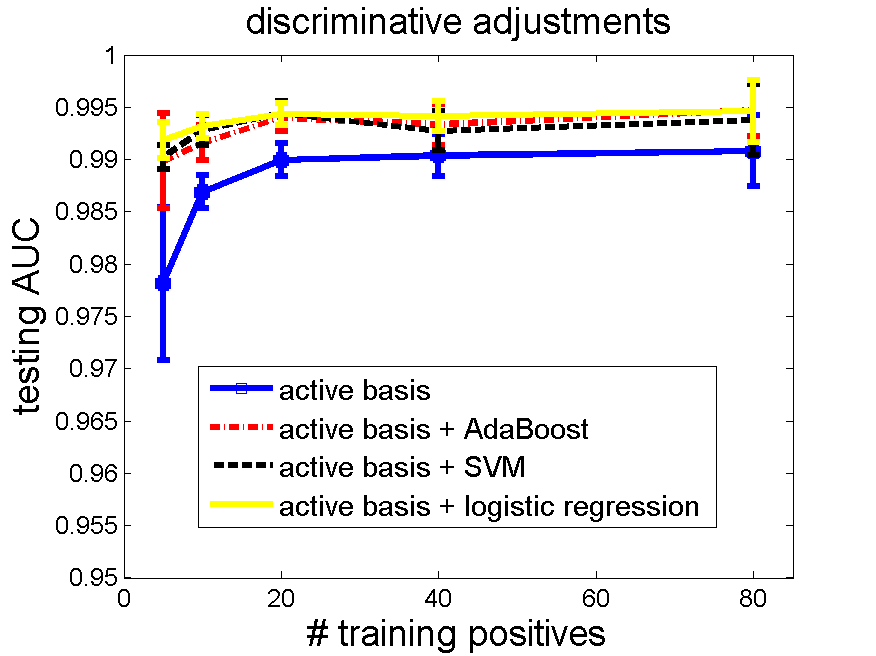
5.3 Motorbike. Data is from Caltech 101 [12]. Number of selected elements 80, training negatives 160, testing negatives 855. code




5.4 Butterfly. Number of selected elements 80, training negatives 160, testing negatives 471. code
Since testing AUC of the butterfly dataset is already over 99.5% for active basis, it is hard for discriminative methods to further improve performance. However, logistic regression is still the best one.




6. More Comments
This project works on supervised learning as a starting point. Its value lies in the promising future for extending to unsupervised learning, rather than merely high classification performances.

For unsupervised learning, the general picture remains the same. We apply generative learning by active basis because it is good at discovering hidden variables, and then discriminative adjustment on feature weights can tighten up the parameters and improve classification performances.


7. Acknowledgments
Thanks to my mentor Prof. Ying Nian Wu and PhD fellow Zhangzhang Si, for their instructions to my project, as well as to my self-developing. I have learned a lot from the project. It is a fantastic summer for me. Also thanks to Dr. Chih-Jen Lin for his liblinear software package and his detailed suggestions about how to adjust the software for our experiment.


References
[1] Wu, Y. N., Si, Z., Gong, H. and Zhu, S.-C. (2009). Learning Active Basis Model for Object Detection and Recognition. International Journal of Computer Vision.
[2] R.-E. Fan, K.-W. Chang, C.-J. Hsieh, X.-R. Wang, and C.-J. Lin. (2008). LIBLINEAR: A Library for Large Linear Classification. Journal of Machine Learning Research.
[3] Lin, C. J., Weng, R.C., Keerthi, S.S. (2008). Trust Region Newton Method for Large-Scale Logistic Regression. Journal of Machine Learning Research.
[4] Vapnik, V. N. (1995). The Nature of Statistical Learning Theory. Springer.
[5] Joachims, T. (1999). Making large-Scale SVM Learning Practical. Advances in Kernel Methods - Support Vector Learning, B. Sch?lkopf and C. Burges and A. Smola (ed.), MIT-Press.
[6] Freund, Y. and Schapire, R. E. (1997). A Decision-Theoretic Generalization of On-Line Learning and an Application to Boosting. Journal of Computer and System Sciences.
[7] Viola, P. and Jones, M. J. (2004). Robust real-time face detection. International Journal of Computer Vision.
[8] Rosset, S., Zhu, J., Hastie, T. (2004). Boosting as a Regularized Path to a Maximum Margin Classifier. Journal of Machine Learning Research.
[9] Zhu, J. and Hastie, T. (2005). Kernel Logistic Regression and the Import Vector Machine. Journal of Computational and Graphical Statistics.
[10] Hastie, T., Tibshirani, R. and Friedman, J. (2001) Elements of Statistical Learning; Data Mining, Inference, and Prediction. New York: Springer.
[11] Bishop, C. (2006). Pattern Recognition and Machine Learning. New York: Springer.
[12] L. Fei-Fei, R. Fergus and P. Perona. (2004). Learning generative visual models from few training examples: an incremental Bayesian approach tested on 101 object categories. IEEE. CVPR, Workshop on Generative-Model Based Vision.
[13] Friedman, J., Hastie, T. and Tibshirani, R. (2000). Additive logistic regression: A statistical view of boosting (with discussion). Ann. Statist.

Back to active basis homepage
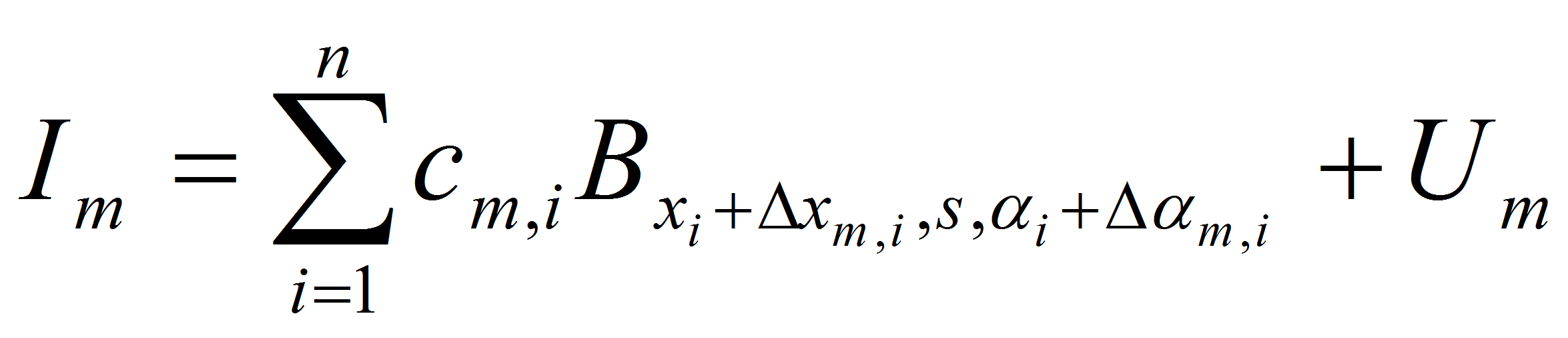
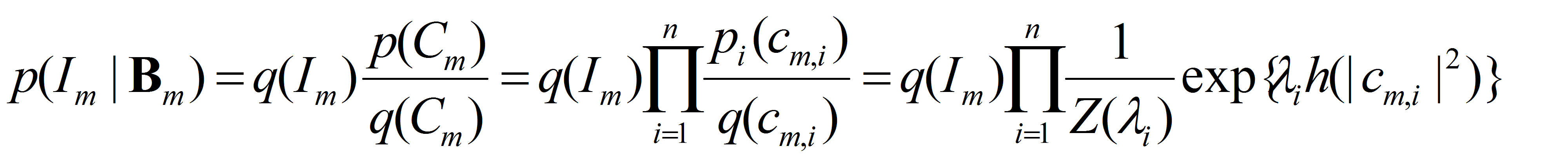
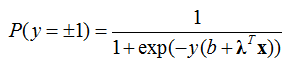
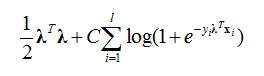
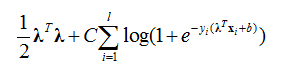